Trigonometric Expressions | ||
| ||
Introduction | ||
In this section, you will learn how to simplify trigonometric expressions. Here are the sections within this lesson:
|
Trigonometric expressions are non-routine appearing problems. They are unfamiliar because the language of trigonometry looks foreign and complicated. In order to learn how to simplify or reduce the complexity of trigonometric expressions, we first need to examine the identities we need to utilize. Rooted within right triangle trigonometry, there are:

The Pythagorean Identities are proven to be true in the following section: Deriving the Pythagorean Identities. These expressions are reciprocal trigonometric identities by definition.
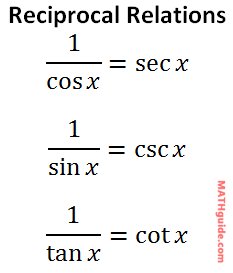
These expressions represent the relationships between tangent and the sine/cosine functions.
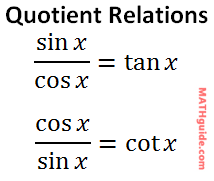
| |
This video will derive the three Pythagorean trigonometric identities. | |
Before proceeding with this lesson, you must understand numerous skills. Those skills that are most needed are knowledge of factoring and rational expressions.
| |
The main goal in dealing with trigonometric expressions is to simplify them. This means large, multiple-function expressions are considered simplified when they are compact and contain fewer trigonometric functions. For instance, this expression is complex.
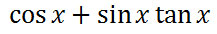
This expression is simple.
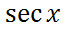
Surprisingly, the two expressions are mathematically equivalent to each other. Before we look at the specifics of how to simplify the complicated expression to that of the simple expression, we need to gain the overarching strategies of working with trigonometric expressions. Here are several strategies for dealing with trigonometric expressions.

| |
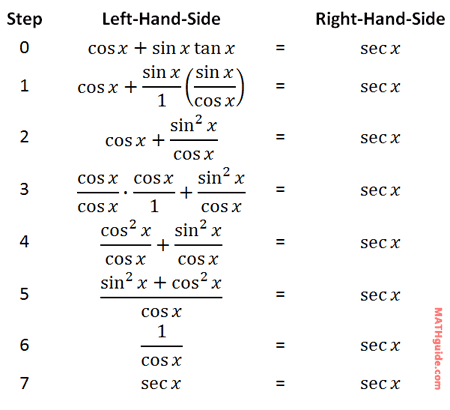
The complex expression from the last section will be our first target for simplification. We will simplify it to show that it is indeed equal to sec x. In doing so, we will be verifying that this equation is valid, which is called verifying an identity.
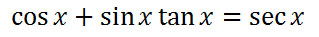
We will focus on the left side of the equation because it is the most complicated side. The first step will be to replace the tangent function with sine and cosine using the first quotient formula.
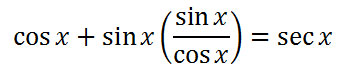
To elicit fraction multiplication, we should view the sine function also as a fraction.
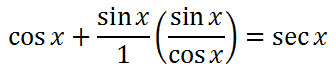
Now, we will multiply the sin x and the fraction next to it. Keep in mind, (sin x)(sin x)= sin2x. This is the result.
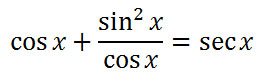
Now, let's use the third step within our strategy list. We need to get a common denominator. The common denominator is cos x. This means we need to multiply the leftmost fraction's numerator and denominator by cos x, like so.
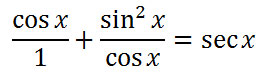
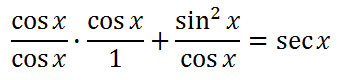
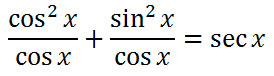
Since there is a common denominator, the two numerators can now be added.
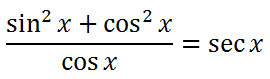
If we take a look at the numerator, we can see it matches the left side of the first Pythagorean Identity.
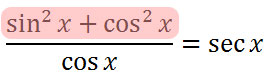

Substituting, we get this.
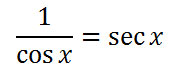
This last fraction can be simplified one more time. Looking at the first inverse relation, we can see that it is equal to sec x.
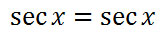
Since both sides have been found to be equal, this is proof that the original equation is an identity and our work is complete. Here are all eight steps listed in order.
Now that you have read a lesson on simplifying trigonometric expressions, watch these videos and try our interactive quiz.
| |
Here is our next trigonometric equation to simplify, which again is called verifying an identity.
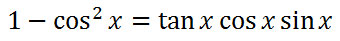
Our first job will require us to take a look at the first Pythagorean Identity.
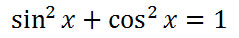
Unfortunately, we need to manipulate it slightly so that it can be of use for us. If we subtract the cosine-squared from both sides, it will be more clear how we can use it.
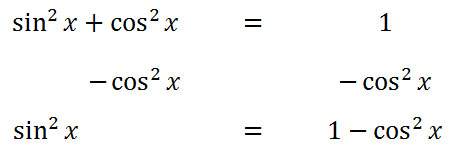
Taking a look at the last step of the process above, we can see this slightly new relationship.
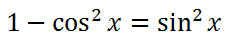
The left side of this new relationship matches up perfectly with the left side of our problem. We are ready to substitute.
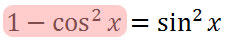
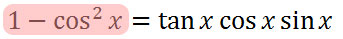
Our new equation becomes this.
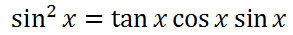
Now, we will simplify the right side of our equation. We will similarly replace the tangent with its quotient identity.
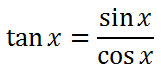
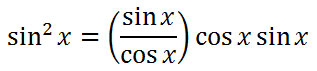
It can be seen that the cosines will cancel.
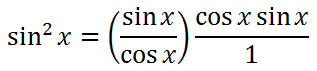
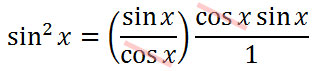
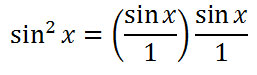
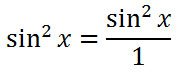
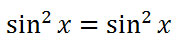
Since both sides of the equation are identical, we have shown that the original equation is an identity and we are done. Here are all the steps written in order without the explanation.
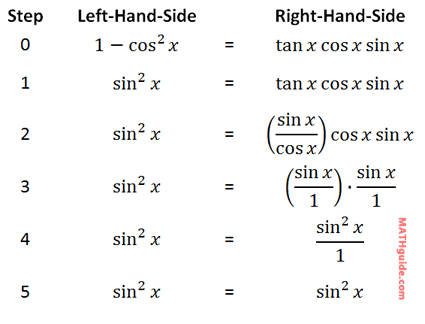
Now that you have read a lesson on simplifying trigonometric expressions, try these videos and interactive quiz.
| |
View this instructional video that will demonstrate how to verify trigonometric identities. | |
Try our instructional videos to help learn this material.
| |
Try our interactive quiz to determine if you understand the lessons above.
| |
Try these activities, which are related to the lessons above.
| |
Try these lessons, which are closely related to the lessons above.
| |
 ideo:
ideo:  esson:
esson:  uiz:
uiz:  ctivity:
ctivity: