The Law of Cosines | ||
| ||
Introduction | ||
Here are the sections within this lesson:
|
Triangles are a fundamental geometrical shape. Triangles appear within several disciplines, some of which are architecture, engineering, astronomy, and chemistry. This is why mathematicians have studied them and consequently have several relations to enumerate their sides and angles. Here is one such relation. These are the equations collectively called The Law of Cosines.
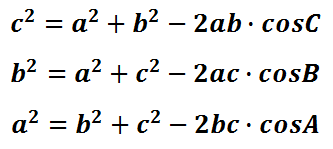 As it will be thoroughly explained within the next section, these equations are useful for two cases: 1) when two sides and the angle between them are known within a triangle and 2) when all three sides of a triangle are known. If either case is known, then the law of cosines is helpful.
If you are not familiar with how to label a triangle or you have never worked with sine, cosine, or tangent, please read our trigonometry basics section before moving on to the next sections within this page.
| |
Let's take a look at some given information within the following diagram. 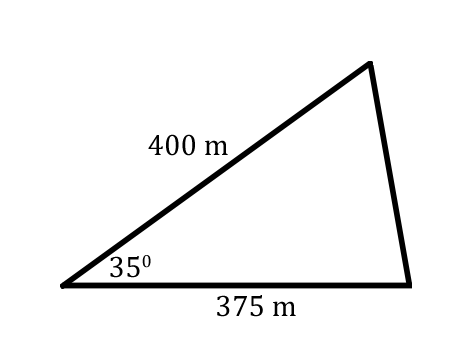 The law of cosines is a helpful tool for this situation because we know a triangle's angle and the sides that are next to it, as emphasized via the colored graphic below.  Now that we know the lawe of cosines can be used for the problem, we now need to label the triangle's angles. The triangle can be arbitrarily labeled with the letters 'A,' 'B,' and 'C.' We will progress with the following arrangement of labeled angles. 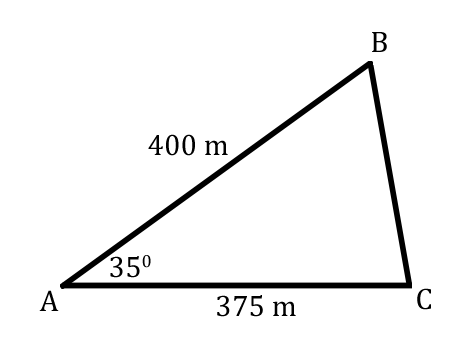 Now we can start labeling the sides. The side opposite angle-A, our 35-degree angle, is side-a. 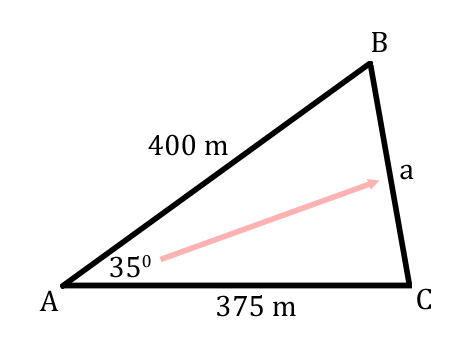 Likewise, side-b is 375, side-c is 400. Using this set of information, we have to determine which law of cosines equation is best to use. Since we know angle-A, we should find the formula that has angle-A in it.
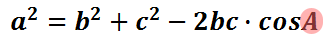 Using this equation, we need to plug in the given information within it.
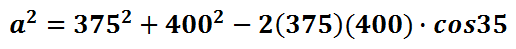 A calculator can be used to simplify the right side of the equation.
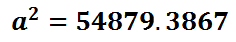 To cancel the square on the right side of the equation, we must employ its inverse function, which is the square root. We will take the square root of both sides of the equation.
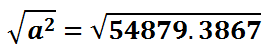 Again, with the use of a calculator, we can find side-a by actually using the square root function of a calculator.
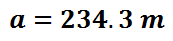 It has been shown that the law of cosines is useful for calculating the side of a triangle when we know two sides and the angle between those sides. The side we calculate will always be the side opposite the given angle Use this video and quiz to reinforce the lesson.
| |
Here is a given situation involving a triangle. 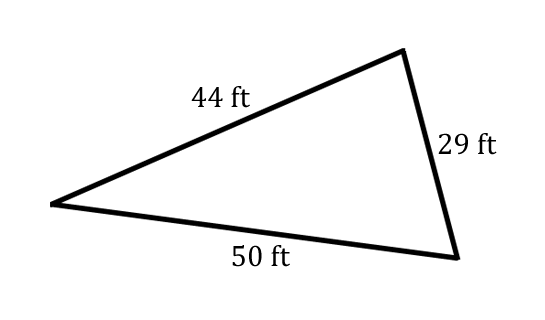 The given information above is one where we know all three sides of a triangle. Let's label the angles with 'A,' 'B,' and 'C.' Labeling the angles is arbitrary; but, for the sake of continuing along with the given information, we will go with this arrangement of angles. 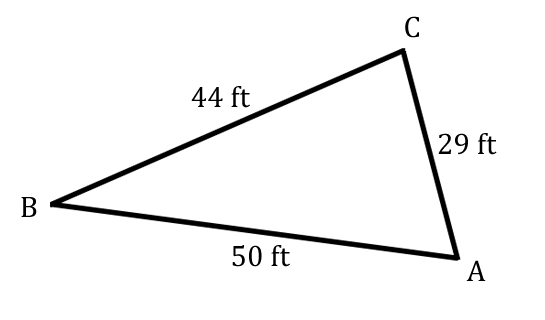 Recall, we look to the sides opposite sides an angle and label them accordingly. For instance, side-c is opposite angle-C. The graphic below demonstrates this labeling of sides. 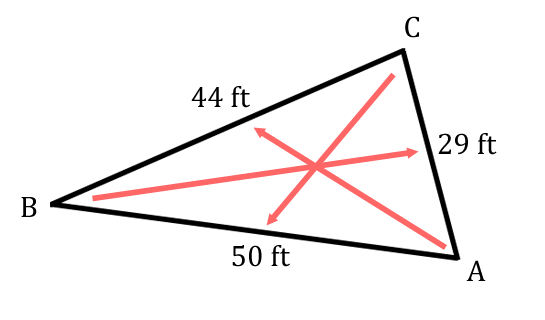 It is now clear that side-a is 44, side-b is 29, and side-c is 50. Our next challenge is determine what we can calculate. The only variables that are unknown are angles. So, we must choose which angle to solve for. We can solve for any of them, making our choice an another arbitrary choice. Let's pick angle-C to find.  There are three law of cosine equations to use. Let's review them.
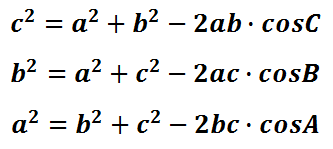 Of the three equations, only one of them contains angle-C. Since we have chosen to solve for angle-C, we will use that equation.
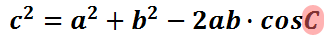 Let's plug in the given information: side-a is 44, side-b is 29, and side-c is 50.
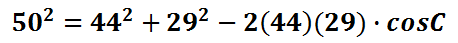 It is now time to start cleaning up the equation so we can solve for angle-C. Let's square the numbers and multiply the factors in front of the cosine function. Doing so will yield this:
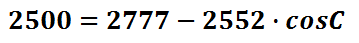 The steps that we have taken so far have been basic. It has involved basic the substitution of values, squaring some numbers, and multiplying factors. Now, we have to tackle some algebra. Commonly, students make an error at this step. Some students think these two numbers can be subtracted. However, these numbers cannot be combined because they are not like terms. Do not make the mistake of combining these values.
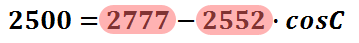 Instead of combining unlike terms, we have to cancel the 2777 by subtracting that value from both sides of the equation.
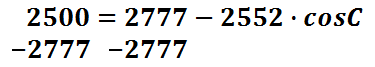 This is the result of subtracting 2777 from both sides of the equation.
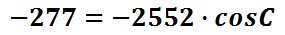 Our next task is to cancel the coefficient. The -2552 must be canceled by dividing that value from both sides of the equation.
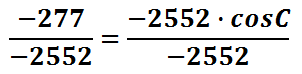 Insead of dividing the right side, let's leave the value as a fraction so that we can avoid rounding a decimal value. It's better to round the value once at the conclusion of our calculations. Doing so will allow us to retain the most accurate answer possible.
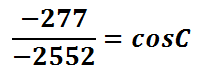 We have nearly solved our equation for angle-C. However, we have the cosine of angle-C. The next step must involve canceling the cosine function. The only way to cancel the cosine function is to use the inverse cosine function, like so.
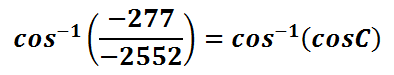 This is what our equation becomes after we cancel the cosine function with its inverse cosine function.
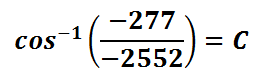 All that remains now is the use of a calculator. We have to place this information into a calculator to get the final value for angle-C.
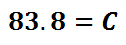 The steps above show how we can arrive at an angle when we are given three sides of a triangle. Use this video and quiz to help you reinforce the lesson.
| |
There are two laws, The Law of Cosines and the Law of Sines (see the Related Lessons section for the lesson). This table will help determine which law to use given the circumstances that are present.

Let it be known to use the Law of Sines we do have to know three pieces of information: 1) we either know two angles and a side or 2) two sides and an angle.
When considering the first case, knowing two angles of a triangle means we can find the third angle. If we know a side, we automatically know the angle opposite that side because we know all the angles of the triangle. For the second case, we must know an angle that is opposite one of the two given sides. Having an angle and a side opposite it is the indicator we must use the Law of Sines.
| |
View these videos to help you learn how to use the Law of Cosines.
| |
This quizmaster will test your skills. Use it to see if you can calculate with The Law of Cosines.
| |
This activity is related to the lessons above.
| |
We would like to invite you to learn from our other advanced trigonometry lesson.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: