The Law of Sines | ||
| ||
Introduction | ||
Triangles are a fundamental geometrical shape. Triangles appear within several disciplines, some of which are architecture, engineering, astronomy, and chemistry. This is why mathematicians have studied them and consequently have several relations to enumerate their sides and angles. Here is one such relation. This is the equation called The Law of Sines.
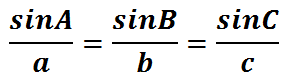 As it will be thoroughly explained within the next section, this equation is useful when a certain angle and its opposite side are known (and either another side or angle) for a given triangle. If this given information is known, then it is possible to calculate another known angle's opposite side or another known side's opposite angle.
If you are not familiar with how to label a triangle or you have never worked with sine, cosine, or tangent, please read our trigonometry basics section before moving on to the next sections within this page.
| |
When solving for unknown sides and angles of a triangle, we must first determine how many triangles exist. Most of the time there is only one possible triangle but there is a special set of circumstances that leads to several options. If we are ever given two side lengths and the angle that is not between the sides, we have to be careful. This case is called Side-Side-Angle (abbreviated as SSA). Depending on the circumstances, there are three cases: a) no triangle can be made, b) one triangle can be made, or c) two triangles can be made. This helpful table can be used to assist us as we determine how many triangles exist.
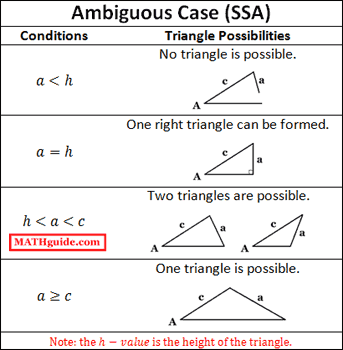 This video will inform you how to use the table and determine how many triangles exist given a SSA situation.
| |
Let's say we are given the following information for a triangle. 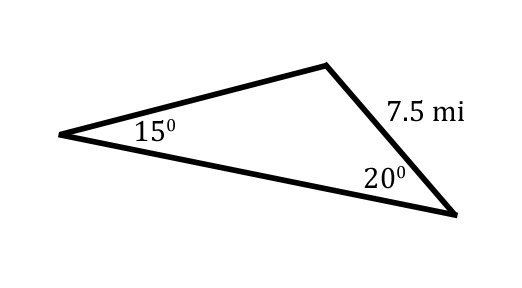 This situation is appropriate for The Law of Sines. The reason it is appropriate is because the 15 degrees and the 7.5 miles are opposite of each other. This is emphasized in the next graphic. 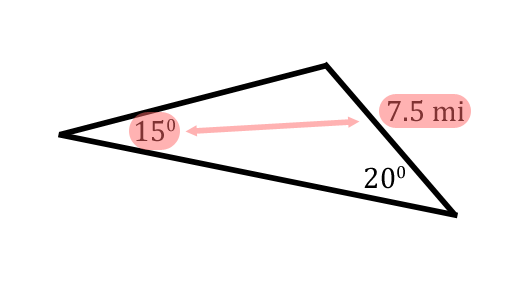 Consequently, we will be able to solve for the side marked with the 'x.' [The angles have been marked with the letters 'A,' 'B,' and 'C.' The labeling is arbitrary and the problem could be solved with any arrangement of the letters.] 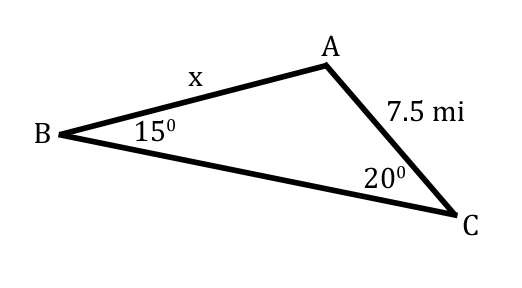 The reason side-x can be calculated is because it is opposite a known angle, angle-C. 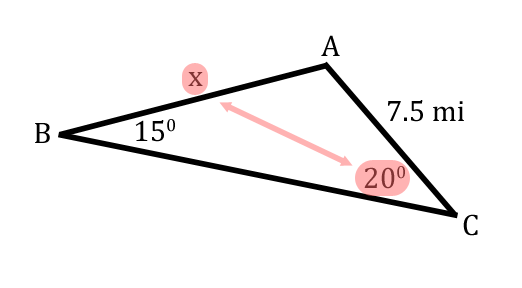 Now we will refer to our equation. The Law of Sines has three ratios — three angles and three sides.
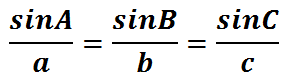 We have only three pieces of information. We also know nothing about angle-A and nothing about side-a. So, we will only need to utilize part of our equation, which are the ratios associated with 'B' and 'C.'
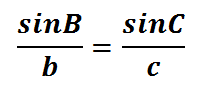 We know angle-B is 15 and side-b is 7.5. We also know that angle-C is 20, but we do not know side-c. We will substitute these values into the equation as such.
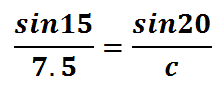 Now that we were able to construct two equal ratios, called a proportion, let's solve it by cross-multiplying.
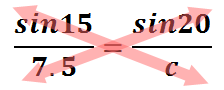 Cross-multiplying will give us these equal products.
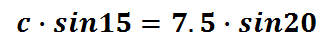 The equal products above make a simple equation. We have to solve for the variable 'c.' To do so, we will have to divide both sides of the equation by the sin 15.
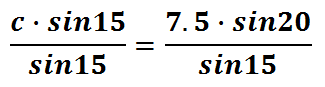 We can cancel the sin 15s because we're both multiplying and dividing 'c' by that value.
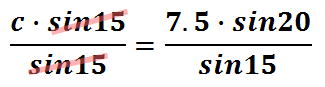 With the sin 15 out of the way, we need to plug this into a calculator.
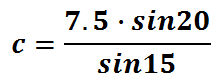 After evaluating with a calculator, this is our final value for 'c.'
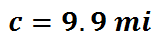 This means the value of 'x' in our problem is 'c' also, which is 9.9 miles. Use this video and quiz to reinforce the lesson.
| |
For our next Law of Sines problem, let's take a look at this given information. 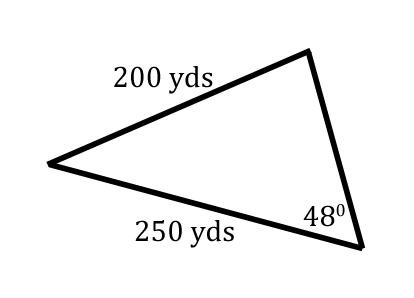 This stuation is ideal for The Law of Sines. We were given a side and it's opposite angle. 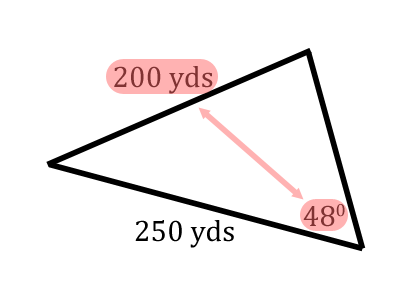 Since we also have another side, we can solve for another angle, which has been marked with a 'y' in this graphic. 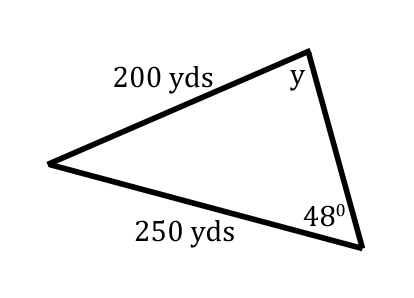 Angle-y rests opposite the 250, which is a known length of our triangle. 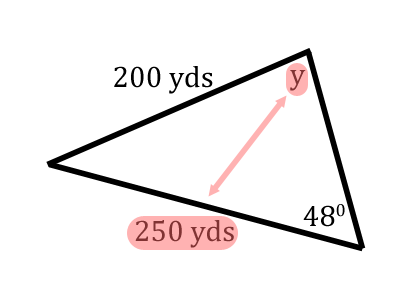 When there are two pairs of opposite sides and angle, we can utilize The Law of Sines. All we have to do now is label the triangle. The triangle below has been arbitrarily labeled with 'A,' 'B,' and 'C.' Any arrangement of 'A,' 'B,' and 'C' can be used; so, we'll stick with this arrangement of letters and angles. 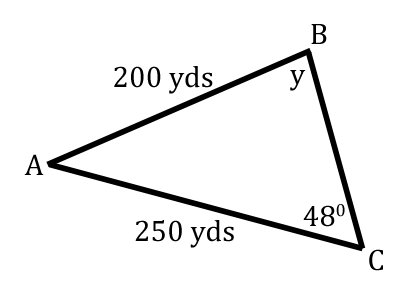 This is when we use The Law of Sines.
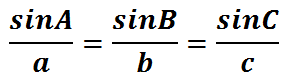 We can see that Angle-C is 48 and side-c is 200. Angle-B is unknown, but side-b is 250. So, we will place these values into the equation. Without knowing anything about side-a and angle-A, we'll use only the ratios that involve 'B' and 'C.'
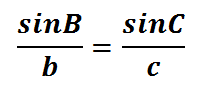 This is what the equation looks like once the appropriate numbers are plugged inside of it.
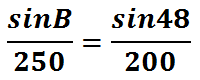 When we have two equal ratios, called a proportion, we need to cross-multiply to advance.
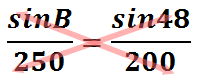 This is what the cross-products look like.
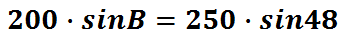 To continue solving for B, we have to divide both sides of the equation by 200.
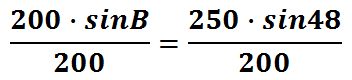 Since we are multiplying and dividing by 200, we can cancel it to get sinB alone.
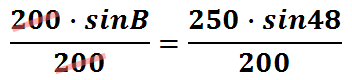 This is what we are left with, the sin of angle-B.
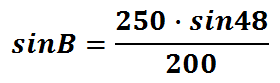 To cancel the sine of angle-B, we have to utilize the inverse sine function.
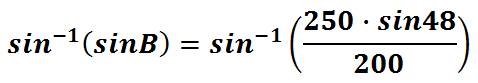 Therefore, this is what we need to plug into a calculator.
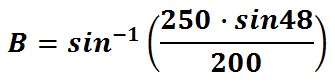 This is our final answer for angle-B.
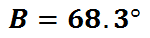 Since we were trying to solve for variable-y, it is also 68.3 degrees. Use this video and quiz to reinforce the lesson.
| |
There are two laws, The Law of Sines and the Law of Cosines (see the Related Lessons section for the lesson). This table will help determine which law to use given the circumstances that are present.

Let it be known to use the Law of Sines we do have to know three pieces of information: 1) we either know two angles and a side or 2) two sides and an angle.
When considering the first case, knowing two angles of a triangle means we can find the third angle. If we know a side, we automatically know the angle opposite that side because we know all the angles of the triangle. For the second case, we must know an angle that is opposite one of the two given sides. Having an angle and a side opposite it is the indicator we must use the Law of Sines.
| |
Try out our videos on this topic.
| |
Try out our quizmaster on this topic.
| |
Try out our quizmaster on this topic.
| |
We would like to invite you to learn from our other advanced trigonometry lesson.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: