Sum & Difference Angle Formula (Tangent) | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about the sum and difference angle formulas for tangent. Here are the topics within this page:
|
The sum and difference angle formula for the tangent function is:
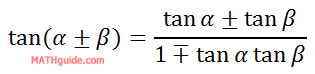
Notice the formula has a plus-minus sign and a minus-plus sign. When we are dealing with a sum of two angles, the numerator will contain an addition sign but the denominator will contain a subtraction sign. The opposite is true when we are dealing with a difference of two angles. In the section called Using the Formula, this will be thoroughly explored.
However, the proof of this formula will be supplied within the next section.
| |
The proof of the formula is straight forward. To begin it, we have to remember this trigonometric identity.
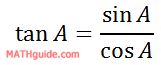
So, start with the sum of two angles within a tangent function and use the above relationship.
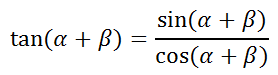
Now, expand the numerator and denominator using the sum angle formulas for sine and cosine [see Sum and Difference Angle Formulas (Sin, Cos)].
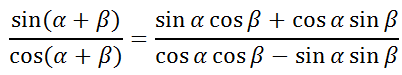
Next, divide the numerator and the denominator by (cosα)(cosβ).
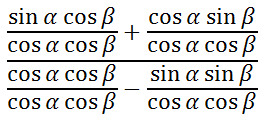
Simplifying the expressions leads to...
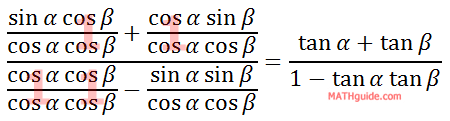
So, this relationship has been established...
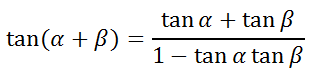
If we substitute -β for β, we get this...
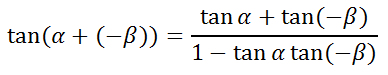
We also should know this relationship.
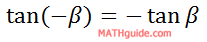
We need to substitute -tanβ for tan(-β).
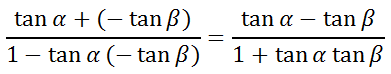
So, we now have these two related equations.
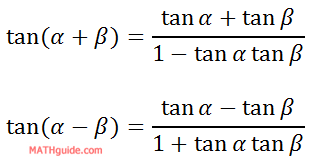
We can merge them together if we notice the pattern with the signs. When there is a sum of angles, the numerator has an addition sign (same sign) and the denominator has a minus sign (opposite sign). This is similar to the denominator, as far as same sign and opposite sign is concerned. Therefore, here are the two equations together with a little sign (plus-minus and minus-plus) ingenuity.
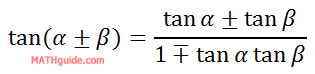
| |
Before continuing on with this section of the lesson, it is extremely important that you understand the unit circle or how to evaluate trigonometric functions at special angles. If you are not familiar with these topics, review the following lessons.
Suppose we wanted to find the exact value of tan(255°). We cannot find this value because it is not a special angle, or can we? Since 255° is the sum of two special angles on a unit circle, it can be done. 255° can be expressed as 225° + 30°, which means we can use the sum formula to evaluate it.
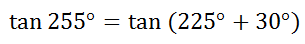
Using the sum formula, we get...
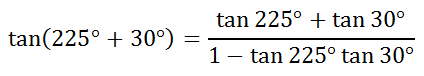
Now, we can evaluate the expression, like so.
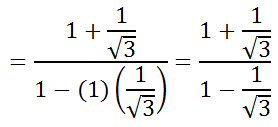
We have to rationalize all fractions that contain a square root. So, we have to multiply those fractions by the square root of 3 over the square root of 3, which is shown below.
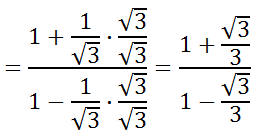
We can also get a common denominator, like this.
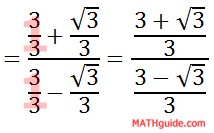
To deal with the complex fraction, change it from division to multiplication, like so.
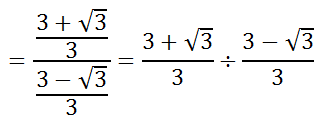
Continuing on...
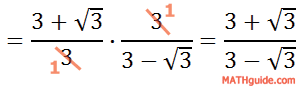
Some students may be allowed to stop here. However, the denominator still contains a square root. To eliminate the square root in the denominator, we have to multiply the denominator and the numerator by the conjugate of the denominator.
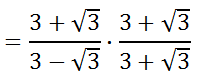
In doing so, we get this.
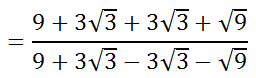
We can clean up the numerator and denominator to get...
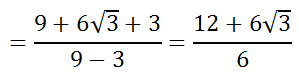
We can factor the numerator so that we can reduce the fraction.
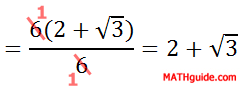
| |
Here are lessons that are related to the content above.
| |
 esson:
esson: