Rational Expressions | ||
| ||
Introduction | ||
In this section, you will learn how to manipulate rational expressions. Here are the sections within this lesson:
|
To understand rational expressions (fractions) that also include variable expressions (letters), it is necessary to have a respectable understanding of fractions that do not contain variables. These lessons/videos may prove useful for those viewers who need to review some basic skills that involve fractions.
| |
Rational expressions are fractions. The word rational is based on the word ratio, which roughly means a comparison or union of two quantities. When we are dealing with a ratio of two values or mathematical expressions, we can simplify the ratio if the numerator and the denominator contain a common factor. Let's look at this example.
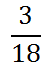 It can be seen that the numerator and the denominator both contain the common factor of three. So, we can divide them both by three, like so.
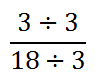 The result of the division is this.
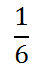 You can gain more detailed examples on how to reduce fractions by accessing this lesson.
The rational expression above is extremely basic. Let's look at a more complicated rational expression, like this one.
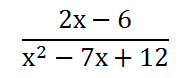 When we simplify this rational expression, we have to be careful how we simplify or reduce the fraction. We can only cancel factors, not sums or differences. In other words, we cannot reduce the 6 and the 12 above. To reduce the ratio, we have to first factor the numerator and the denominator. If you are unfamiliar with factoring, please review our lesson of factoring before continuing on. However, we can factor the numerator, because both the terms there are divisible by 2. The denominator can be factored as a product of two binomials, like so.
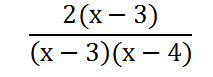 Once factored, we can see now that the numerator and the denominator both contain the common factor, namely the x - 3.
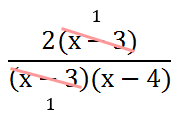 This leaves us with a much more simplified rational expression.
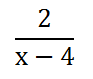 Again, we have to be careful not to get overzealous with our canceling. Keep in mind that we can only cancel factors, not parts of sums and differences. Since we cannot divide the entire denominator by 2, we cannot reduce the rational expression by a factor of 2. | |
To understand how to multiply rational expressions that contain variables, first you have to know how to deal with fractions that contain no variables. Use this lesson if your skills with fractions need some help.
This video will demonstrate how to multiply rational expressions.
| |
To understand how to divide rational expressions that contain variables, it is necessary to know how to divide fractions that contain no variables. Use this lesson if your skills with fractions require help.
This video will demonstrate how to divide rational expressions.
| |
Before progressing with this section, make sure that you already understand how to add fractions that do not include variables. Review this lesson, first.
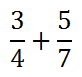 To add fractions, we first need a common denominator. To get an idea of what that common denominator can be, let's look at multiples of 4 and 7.
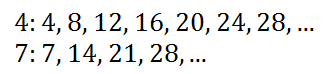 You can see that the two denominators have a common multiple. That common multiple is 28.
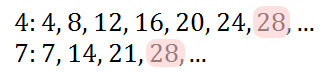 To gain the common denominator, we will multiply the top and bottom of the first fraction by 7. We will multiply the top and bottom of the second fraction by 4.
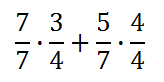 After performing the multiplication, this is what we get.
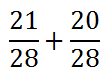 Now we can add the numerators, 21 and 20, to get 41. This takes us to our final answer.
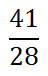
Here is a problem that involves two complex rational expressions, otherwise known as ratios or fractions. We are being asked to add them.
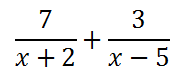 To start, we have to get a common denominator. The common denominator can be obtained by multiplying the two denominators x 5 and x + 2 together. This means the denominator on the left needs to be multiplied by x 5. The denominator on the right needs to be multiplied by x + 2.
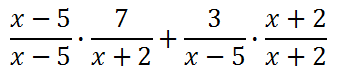 Notice that I didnt just multiply the denominators by these factors. When multiplying the fraction, we also have to multiply the numerator by the same amount. In doing so, we are actually multiplying the fractions by 1s. Multiplying by 1 does not change the value of the original fractions.
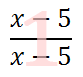
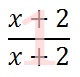 Now that we determined what factors to use to get a common denominator, we now have the job of actually multiplying the factors.
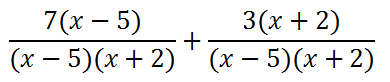 Doing the distributive property, we will multiply the factors in our new numerators:
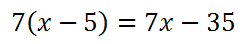
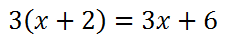 So, our new problem will be transformed using those expressions within the new numerators.
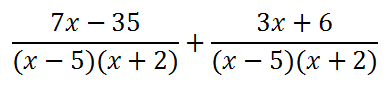 Since the denominators are now both equal to each other, we can add them. Adding fractions with equal denominators requires us to add the numerators and keep the same denominator, like so.
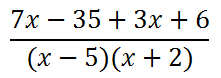 Finally, we need to add like terms. This is now our final answer below.
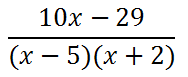 MATHguide offers a free quizmaster to test your skills and determine if you can apply them on a new problem. Use this link to use our Adding Rational Expressions quizmaster.
| |
Before progressing with this section, make sure that you already understand how to subtract fractions that do not include variables. Review this lesson, first.
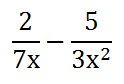 Like the addition problem above, we need to get a common denominator. When we look at the 3 and the 7, their common multiple is 21. However, we also need to deal with the letters. If the 'x' is multiplied by 'x,' then the result will be x2. So, a common denominator can be gained with both the letters and the numbers. We will multiply the first fraction's numerator and denominator by 3x. We will multiply the second fraction's numerator and denominator by 7. This is what that multiplication looks like.
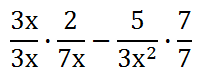 When we multiply (3x)(2) = 6x. Likewise, (5)(7) = 35, (3x)(7x) = 21x2, and (3x2)(7) = 21x2. Consequently, this is the result of the rational expressions.
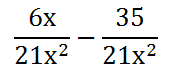 Now that we have a common denominator, we can subtract the numerators, as follows.
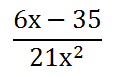 The numerators 6x and 35 are not like terms. Therefore, they cannot be combined. The expression above is the final result. Now, try the following interactive quiz to test your skills. See if you are able to subtract two rational expressions.
| |
We have seen how to simplify, add, and subtract above. Now we will look at a more advanced problem, like the one below.
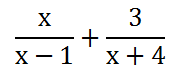 This problem is more difficult because the denominators are complex. However, finding a common denominator in this situation is still possible. To gain a common denominator, we can simply multiply one denominator by the other. In other words, we can multiply the numerator and denominator of the first fraction by x + 4 and we can do similarly with the second fraction, but use x - 1.
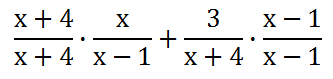 So, now we have to multiply x(x + 4) and multiply 3(x - 1).
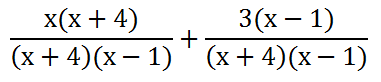 If we multiply, we get x(x + 4) = x2 + 4x and 3(x - 1) = 3x - 3.
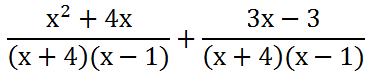 Since we have a common denominator, we can combine the numerators.
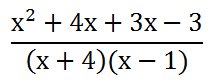 We can also combine like terms, namely the 4x and the 3x to get 7x.
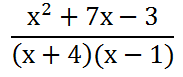 We can either leave the answer in the form above or we could multiply the factors in the denominator.
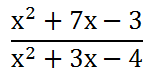 The reason why we cannot simpify the expression further is because the numerator and the denominator contain no common factors. Therefore, we are done and this is our final solution. Now, try the following quizmaster to determine whether or not you grasp this advanced lesson on combining rational expressions.
| |
View this video that demonstrates how to graph a basic level problem. It explains the basics: how to locate and graph the horizontal and vertical asymptotes and how to graph the curve.
This video demonstrates how to graph the same type of rational functions but does so by approaching them as transformations.
| |
This video demonstrates the necessity of factoring in order to locate asymptotes. The rational function in this video has three asymptotes.
| |
This video demonstrates the prelude to several hefty steps: locating holes in a graph, locating vertical and horizontal asymptotes, and sketching the final curve.
| |
Let it be known there is a special case when dealing with ratios, otherwise known as fractions. We cannot divide by zero. Calculators give us errors when we do it, computer programs fail when we tell them to do it, and math teachers tell us to stop doing it. This video will explain why division by zero is graphically and numerically illogical.
| |
These instructional videos will demonstrate how to do the lessons above.
| |
Use these quizzes to test your knowledge of rational expressions.
This quizmaster uses distance, rate, and time along with rational expressions. For that reason, it is a difficult problem. | |
The following lessons below relate to rational expressions. Please visit these lessons to gain a greater understanding of this broader mathematical language.
This lesson can serve as a review on how to factor, which is a skill used when simplifying rational expressions.
| |
 esson:
esson:  uiz:
uiz:  ideo:
ideo:  uiz:
uiz: