Sum & Difference Angle Formula (Sine, Cosine) | ||
| ||
Introduction | ||
In this section of MATHguide, you will learn about the sum and difference angle formulas for sine and cosine. Here are the topics within this page:
|
The angle sum and difference formulas for sine and cosine are:
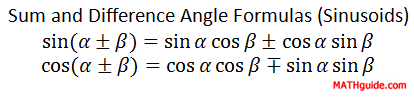
| |
There are several proofs that exist of these formulas. The video in this section provides one of them.
| |
Before proceeding with the following sections, it is strongly recommended that you first understand either special triangles or the unit circle. The links to videos below are provided for that purpose.
The sum/difference formulas enable us to hand calculate more angles than those found on the Unit Circle. However, we have to use the angles on the unit circle. For instance, we can calculate sin (75°). We can do so by looking at the 75° as 45° + 30° or 135° - 60°. To complete the calculation, we would use the sine formula for addition. This will be our first example. Example 1: Find the exact value of sin (75°). We have to find two angles on the unit circle that either add or subtract to 75°, like 75° as 45° + 30°. Now, we must use the formula for sine, like so.
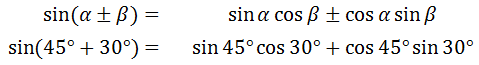
Using our knowledge of either the unit circle or special triangles, we get these ratios for the trigonometric functions on the right side of the relationship.
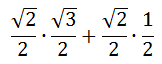
Cleaning up the expression, we get...
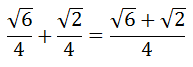
That is the final answer. Example 2: Find the exact value of cos (195°). By trial and error, we can look for a sum or difference of two angles on the unit circle that result with 195°. One result is 135° + 60°. Using the cosine formula for addition, we get this ...
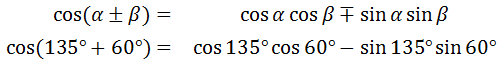
Notice that the left side of the equation has a sum but the expanded formula on the right side of the equation has a minus sign. The cosine formula is strange in this regard. The left side and the right side of the equation will always be opposites like this when we start the problem. Now, we need to evaluate the four trigonometric functions on the right side of the equation.
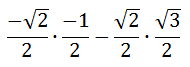
Moving on with Order of Operations, we get...
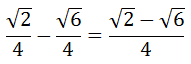
| |
The last section showed two problems moving forward: starting with an angle, finding an appropriate sum/difference, using the formula to expand the sum/difference, and so on. Working backwards requires a slightly different skill set. Examine this example to learn those skills. Example: Write the expression cos49° cos34° - sin34° sin49° as a single trigonometric function in simplist form. The first step is to determine which of the formulas to use. Notice the problem follows a cosine-cosine sine-sine pattern, which makes this either a sum/difference cosine problem. Now that we know which formula to use, we have to make sure the problem is written in the proper form. Looking at the angles, it does not yet exactly fit the pattern of the cosine formula because the angles have to be arranged in this sequence: alpha, beta, alpha, beta. Currently, the angles are arranged, 49°, 34°, 34°, 49°. To solve this dilemma, we can flip the order of the second product from ...
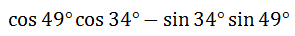
...to...
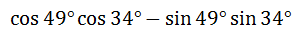
We can do this because we can multiply in any order. The following equation informs us of the equivalent expressions.
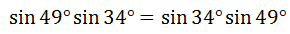
Now, we can place our equation right underneath the formula to see the pattern.
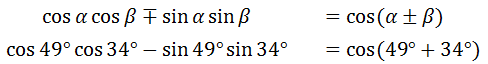
Last, we clean up the sum to arrive at the final solution.
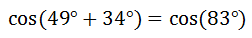
| |
View the following instructional video. | |
This quiz will check for your understanding. | |
Here are lessons that are related to the content above.
| |
 ideo:
ideo:  ideo:
ideo:  esson:
esson: