Work Problems | ||
| ||
Introduction | ||
In this lesson, you will learn how to solve work problems. Work problems are those that involve the speeds of people and/or machines. We will teach you how to calculate how long it will take for multiple workers to perform a job. This lesson is broken down into three sections:
| ||
In order to delve into work problems, it should be understood why it is we study them:
| ||
There is a basic principle related to work problems that must be dealt with. It is the formulation of work in a given unit of time. This question will demonstrate the need to know this basic skill:
If Bridget needs three hours to paint a room, how much work will she get done in an hour of time?To solve this problem, we will have to divide a single job into parts. We will divide the job into three equal parts, which wil be one part for each hour being worked as follows:  The total job can be represented as being a single job, which translates mathematically to a "1." Consequently, each hour of the job must constitute a third of the job, assuming Bridget works at the same speed throughout the entire job. This is appropriate because 1⁄3 + 1⁄3 + 1⁄3 = 1. Now, if the question was changed so that it took five hours to do the job, we would see... 1⁄5 + 1⁄5 + 1⁄5 + 1⁄5 + 1⁄5 = 1. To fully understand this relationship, we should realize a three-hour job requires 1⁄3 of the work to be completed per hour. A five-hour job demands that 1⁄5 of the job gets handled per hour. Using mathematical terms, this relationship is called the reciprocal. So, a seven-hour job would translate to 1⁄7 of the work completed per hour.
| ||
While solving work problems, we will encounter a certain type of equation. The equations are called rational equations because they involve fractions. Here is one type of rational equation.
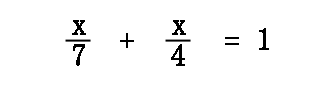 To solve this equation, see what happens when we multiply all the terms of this equation by the denominators. If we multiply all the terms by seven and four, we get this equation.
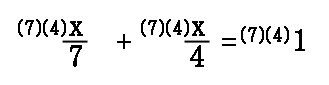 We can cancel factors when a denominator and numerator contain the same factor, as shown in this next step.
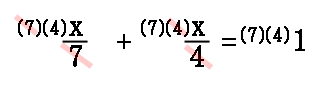 After canceling on the left side and multiplying (7)(4)(1) on the right side, we get this remaining equation.
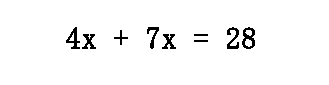 Now, we need to combine terms on the left side to get this next step.
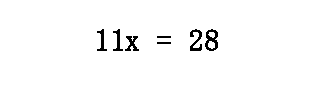 Our last step involves dividing both sides by 11. So, the final answer is x = 2.5454 in a repeating pattern, which rounds to...
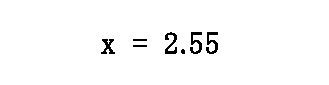 As we can see, when the denominators were canceled, the remaining equation is easily solved.
| ||
Work problems arise from situations revolving around time management. Managers and businessmen solve problems like this one in order to plan or decide if workers are performing at their full potential.
Nancy can paint a fence in 3 hours. It takes Ben 4 hours to do the same job. If they were to work together to paint a fence, how long should it take?First, we will be organizing information and placing the information within a table. This is the table we will be using.
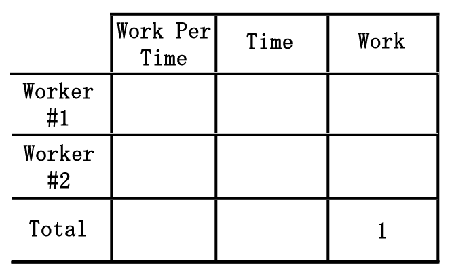 Notice how the table includes a "1" within the bottom row. The "1" stands for the single job that will be completed and it is a standard for all work problems. Second, we need to start filling the table. Discussed within the work basics section, we will formulate the amount of work they do within one hour. We do this by finding the reciprocals of their work times. For Nancy, the reciprocal of 3 is 1⁄3. For Ben, the reciprocal of 4 is 1⁄4. These new figures will be placed within the "Work Per Time" column.
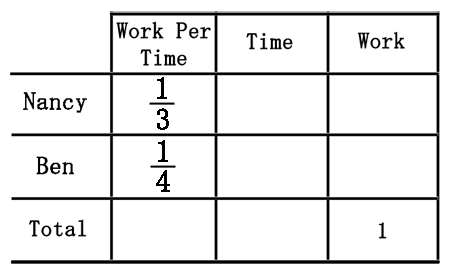 We would like to know how long they need to work together to finish the job. Since they will both begin and end at the same time, they will work for the same amount of time, which is known. So, we will call this unknown "x" and place it within the table.
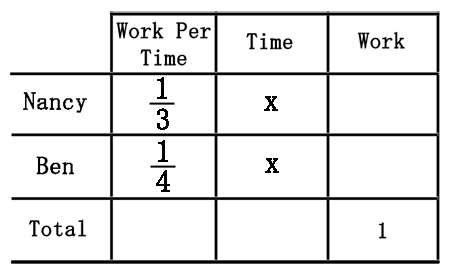 The next step to solving this problem demands that we find values for the last column, "Work." Imagine if Ben worked for 2 hours. We would multiply 1⁄4 times 2 and get 1⁄2, which would mean only 1⁄2 of the job was done. So, if we multiply "Work Per Time" times "Time," we will gain "Work" within our table.
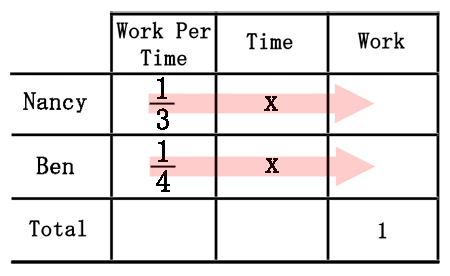 We will multiply across and represent work as algebraic expressions for each row.
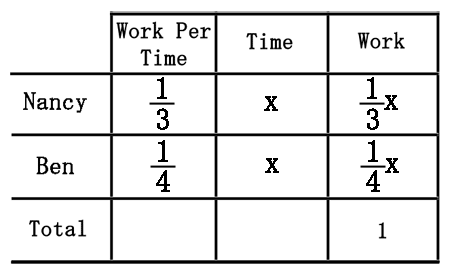 Last, we need to develop an equation to solve this problem. We can get an equation if we think of Nancy and Ben's combined work effort. They are working together to get one problem done. Therefore, the last column holds the equation.
 The sum of Nancy and Ben's work must be set equal to "1" for one job.
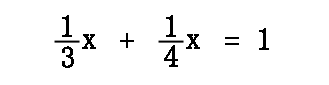 As was done within the solving simple rational equations section, we will follow the same steps. We will multiply all the terms by "3" and "4" to get...
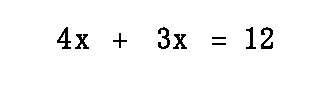 Continuing on by adding like terms, we get this next equation.
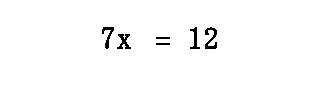 After we divide both sides of the equation by "7," we get this solution once it is rounded to the nearest thousandth.
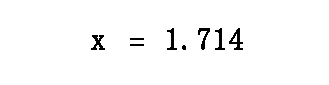 This means if Nancy and Ben work together, they will take 1.714 hours to do the job. This equates to 1 hour and 0.714(60) minutes or 1 hour and roughly 43 minutes to do the job.
| ||
After reading the lessons above, watch this advanced work video that addresses situations when workers start a project at different times.
| ||
There are situations when a worker's individual work time is unknown. This video will demonstrate how to solve for that work rate when the person works with someone else to complete a job.
| ||
These are the instructional videos within the lessons above.
| ||
After reading the lessons above, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
| ||
Here are related lessons to the lessons you viewed above.
| ||
 uizmaster:
uizmaster:  ideo:
ideo:  esson:
esson: