Chemistry Problems | ||
| ||
Introduction | ||
In this section, you will learn how to solve chemistry problems. The information presented here will include steps on how to: deal with percents, organize information, and algebraically mix chemicals using an equation. The sections within this lesson are:
| ||
There are numerous careers that deal with the mixing of chemicals. So, it is important to know how to mathematically handle chemistry problems in order to understand what they mean and how to prepare specific quantities of chemicals. For instance, if 5 liters of 15% hydrogen peroxide (H2O2) solution was in a container, we should be able to determine the actual amount of acid there is in the solution. It turns out, only 15% of the solution is acid; the rest is water. To best handle this mathematically, using a table will help. The table below will help us organize information.
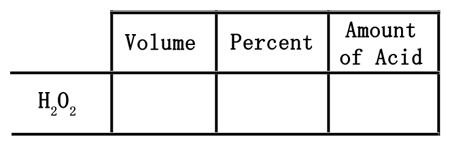 When dealing with 5 liters of a 15% solution, the 5 liters is a volume. The 5 liters needs to be placed in the volume column.
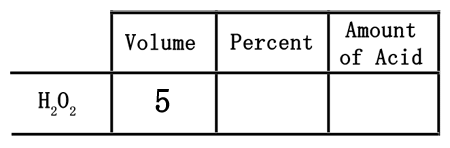 The 15% represents the strength of the acid solution. The greater the percent, the stronger the solution. When placing the percent into the table, first convert it to a decimal. Since percent means "out of 100," we need to divide the 15 by 100 to get 0.15. This number must be placed under percent.
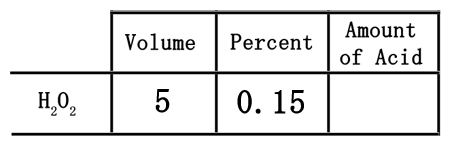 The neat part of using this table is that it can be useful to get the actual amount of acid in the solution. The table has been set up so that the acid can be found by multiplying across, which means multiplying the 5 times the 0.15.
 Since 5 times 0.15 is equal to 0.75, we need to place the 0.75 into the table under the amount of acid.
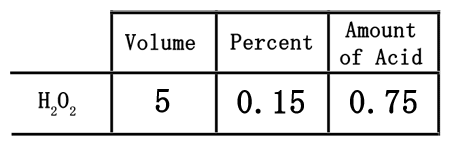 The table helped us to determine that 5 liters of a 15% solution contains only 0.75 liters of acid. This must mean the rest of the solution, or 4.25 liters, must be water.
As we will see in the following section, this process is important for solving problems that combine chemical solutions.
| ||
Since chemistry basics explained the connection between a solution's volume, concentration, and amount of acid, we will use a table to best organize the information found within a problem like this:
If 50 liters of 12% hydrochloric acid (HCl) is mixed with 80 liters of 40% hydrochloric acid, how much acid would result and what would be the concentration of the final solution?First, this is the table that will be used to solve the problem.
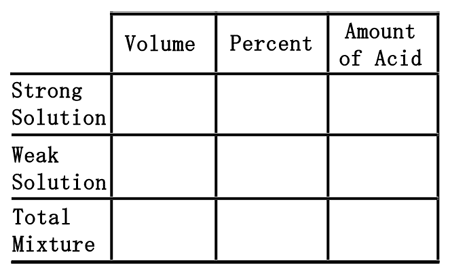 Second, we will divide the two mixtures into a strong acid, 80 liters of the 40% acid, and a weak acid, 50 liters of the 12% acid. We will place their volumes into the table in their respective places.
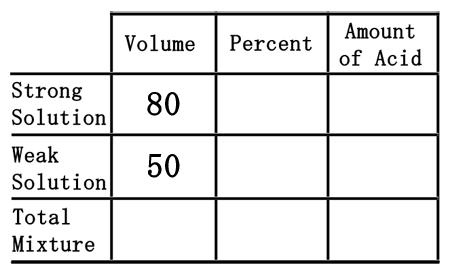 Third, we need to place the percent values into the table. To do so, we must first convert the percents into decimal numbers. Since percent means "out of 100," we will divide the percent numbers by 100. The strong solution percent of 40% will be 40 divided by 100, which is 0.40. The weak solution will be 12 divided by 100, or 0.12.
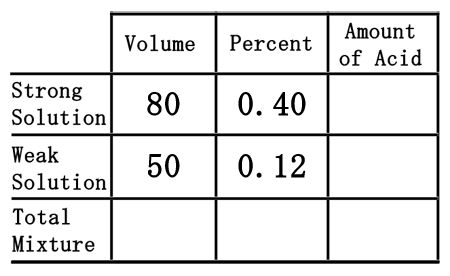 As was the case in the chemistry basics section, we have to multiply across the table to gain the amount of acid.
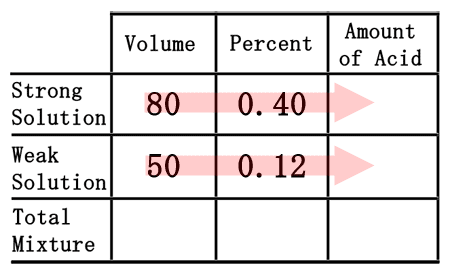 80 times 0.40 is 32. Likewise, 50 times 0.12 is 6. So, we will place these quantities into the table where they belong.
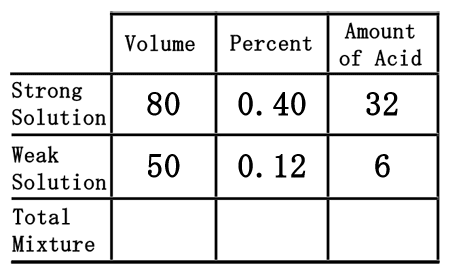 The last row of the table, the "total mixture" row, must now be filled in. We can fill in the "volume" and "amount of acid" portions because mixing the strong and weak acids will result with the total mixture. So, the total volume and the total acid is equal to the sum of its parts. This means we can get the numbers by simply adding down the table for those two columns.  80 plus 50 is 130, for the volume. 32 plus 6 is 38, for the amount of acid. Now, we will place those numbers into the table.
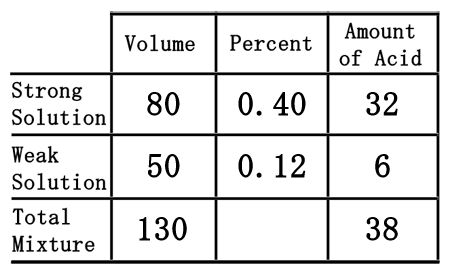 As we saw from the chemistry basics section, we get the amount of acid by multiplying volume times the percent (as a decimal number). Conversely to get the percent number, we will divide the amount of acid from the volume.
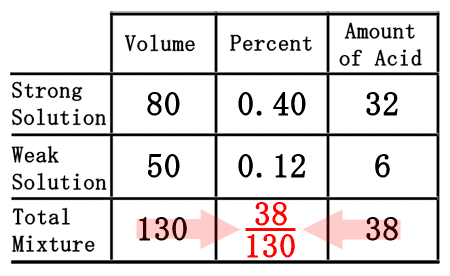 When we divide 38 by 130, we get 0.2923, which rounds to 0.29.
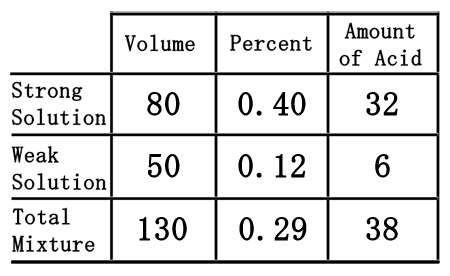 We need to convert the 0.29 to a percent by moving the decimal two places to the right, to get 29%. By reviewing the lowest row of the table, we can now find the solution to our problem. The solution is the total mixure, which states there are 130 liters of 29% HCl.
| ||
The chemistry I section used a table to solve the mixture of two chemicals. We will use the same table to solve a problem like this one: How much 10% sulfuric acid (H2SO4) must be mixed with how much 30% sulfuric acid to make 200 milliliters of 15% sulfuric acid?First, this table will be used.
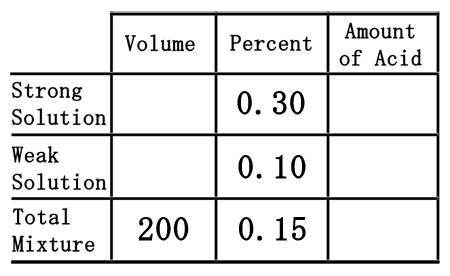
 Second, we have to deal with two solutions of sulfuric acid. We have a weak solution, the 10% solution, and a strong solution, the 30% solution. So, we will place them in the correct places within the table as decimal numbers. 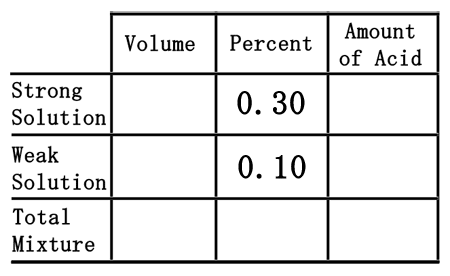 Third, we need to place one last pieces of information into the table, namely the 200 mL of 15% acid we need to make. We will place the 200 mL under the volume column, but in the total row, and the 15% in the percent column as a decimal number.
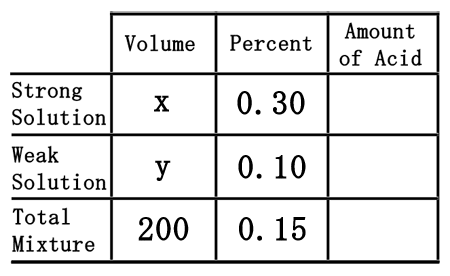
 The difficult part of this problem is figuring out how to deal with the empty spaces within the table. To do that, we will assume we need "x" mL of the strong solution and "y" mL of the weak solution.
 As was done in the chemistry basics section, we need to multiply across the table to calculate the amount of acid for each solution, including the total mixture.
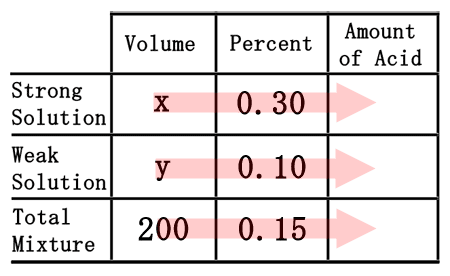 We will need to remember a little algebra for this next part. Multiplying the "x" times the 0.30 will yield 0.30x. Likewise, "y" times 0.15 gets us 0.15y. The 200 times the 0.15 is 30. This is what the table should now look like once filled. 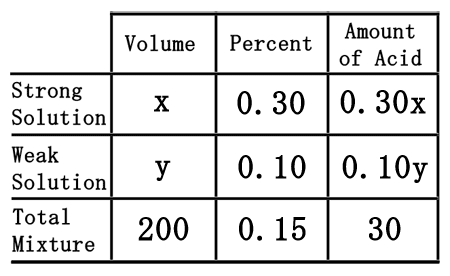 Now that the table is filled, we can use it to get two equations. The "volume" and "amount of acid" columns will let us get two equations.
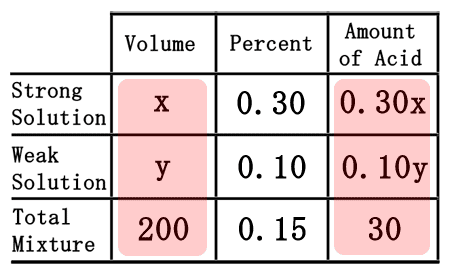 The total volume of the solution must be equal to the sum of the volumes we are mixing. This means "x" plus "y" must equal 200. The same must be true for the acid. The acid we mix must be combined to get the total acid; so, 0.30x plus the 0.10y must equal to the total amount of acid, which is 30. This gives us a system of linear equations. 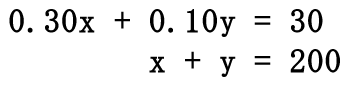 Solve this system of equations by any means to get the solution, (x, y). The solution to the system is (50, 150), which is left to the reader to perform. [A review of the multiplication/addition (elimination) method or substitution method can help obtain this solution.] This means to create 200 mL of a 15% solution, we must use "x" mL, or 50 mL, of the strong solution (30%). The weak solution (10%), or "y," that must be used is 150 mL.
| ||
This activity is a self-guided, asynchronous lesson. The lesson involves watching a MATHguide video, answering in-depth questions, and using a MATHguide quizmasters to assess for understanding.
|
Watch our video on this lesson.
The following video is a fully functional, self-guided lesson. The video instructs how to use the organizational table along with a TI-Nspire calculator. It also provides a link to an accompanying activity.
|
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
|
 uizmaster:
uizmaster:  ideo:
ideo:  ctivity:
ctivity:  esson:
esson: