Distance, Rate, Time Problems | ||
| ||
Introduction | ||
In this section, you will learn how a polynomial's zeros, factors, and graph are all related. Here are the sections within this lesson:
|
The distance problems we will see will require us to know how these variables are related:
Distance When traveling a certain distance, it is done at a certain speed (rate) for a certain length of time. The formula that ties these variables together is…
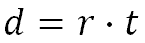
The examples below will demonstrate how this formula works.
| |
Here are some examples of basic distance problems. Example 1: “A man has to bicycle 30 miles. He will travel at 6 mph. How long will it take?” The distance is 30 miles and the rate is 6 mph. We will plug these values into the formula, like so.
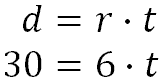
To solve it, we need to divide both sides by 6.
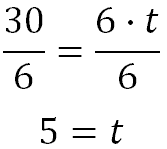
This means it will take 5 hours.
Example 2: “A bug travels at a rate equal to 3 inches per hour. How far will it travel in 4 hours?” The rate is 3 inches/hour and the time is 4 hours. We will plug these values into the formula, like so.
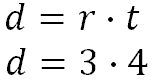
To solve it, we need to simply multiply the values.
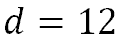
This means it will travel 12 inches.
Example 3: “An asteroid travels 300,000 miles in 4 hours. How fast was it traveling?” The distance is 300,000 miles and the time is 4 hours. We will plug these values into the formula, like so.
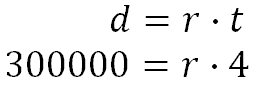
To solve it, we need to divide both sides by 4.
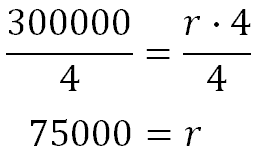
This means it was traveling at 75,000 mph.
| |
Sometimes two objects travel to cover a certain distance. They either travel toward or away from each other, yet the combined distance is of importance. To solve these types of problems, we should make a diagram to aid us in understanding what is happening. Here are two examples. Example 1: “Two skateboarders, Ron and Bob, are traveling in opposite directions. Ron travels at 8 feet per second and Bob travels at 10 feet per second. How long will it take before they are 2640 feet (1/2 mile) apart?” To understand this, we need to represent this skateboard situation using arrows. We’ll give Bob the larger arrow because he is traveling quicker than Ron. After 1 second, they will be 8(1) + 10(1) = 8 + 10 = 18 feet apart.
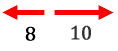
After 2 seconds, they will be 8(2) + 10(2) = 16 + 20 = 36 feet apart.

After x seconds, they will be 8(x) + 10(x) = 8x + 10x = 18x feet apart. When will 18x be equal to 2640? If we can answer this, then we can get an answer to our problem. All we need to do is use algebra.
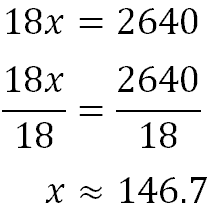
Ron and Bob will have to skateboard for 146.7 seconds to be 2640 feet apart. As a side note, we can change this distance to minutes to get a better idea of this measure of time. Since there are 60 seconds in a minute, we only need to divide by 60 to get 2.4 minutes or almost 2 and a ½ minutes.
Example 2: “Two friends, Sherry and Fredrick, live 2000 miles apart. They want to meet each other and decided to both travel so that they can see each other sooner. If they both drive directly toward each other and Sherry travels at 50 mph and Fredrick travels at 60 mph, how much time will pass before they meet each other?” To understand this, we need to represent this situation using arrows. We’ll give Fredrick the larger arrow because he is traveling quicker than Sherry. After 1 hour, they will have traveled 50(1) + 60(1) = 50 + 60 = 110 miles. This means they will be 2000 – 110 = 1890 miles apart.

After 2 hours, they will have traveled 50(2) + 60(2) = 110 + 120 = 230 miles. This means they will be 2000 – 220 = 1780 miles apart.

After x hours, they will have traveled 50(x) + 60(x) = 50x + 60x = 110x miles. This means they will be 2000 – 110x miles apart. They will meet when they are zero miles apart. When will 2000 – 110x be equal to 0? If we can answer this, then we can get an answer to our problem. All we need to do is use algebra.
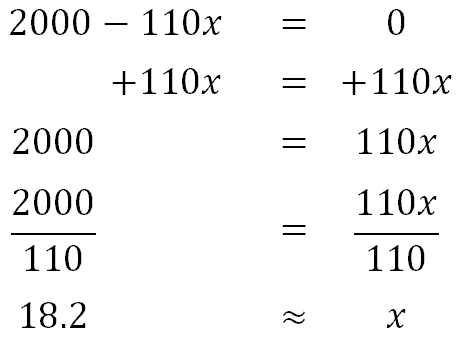
Sherry and Fredrick will have to drive for 18.2 hours before they meet. Now, try our quizmaster to check for understanding.
| |
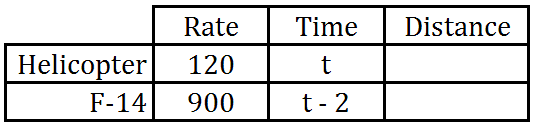
Young kids chase each other when they play. If a slower moving youth chases a faster moving child, there’s no hope for the two ever to meet. However, if a fast-moving child chases a slow-moving child, one will catch the other. It is only a matter of time. These types of problems are crucial for serious problems, too, like logistical problems concerning combat. Let us examine two problems and the methods used to solve them. Example 1: “A helicopter travels to the East going 120 mph. Two hours later, it is determined that the helicopter will need to be escorted on its journey to the East. How long will it take an F-14, traveling at 900 mph to catch up with the helicopter?” To help organize this information, it is best to use a table, like this one.
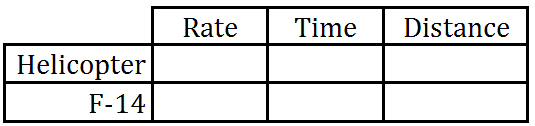
We need to plug in some obvious values, like rates.
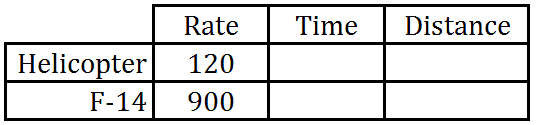
The hard part is correcting for time. We know the helicopter started traveling first, yet it will be traveling for an unknown length of time. However, the fighter plane waited for 2 hours before traveling. Even though we do not know how long the fighter plane will travel, it certainly will travel 2 fewer hours than the helicopter. So, we will use “t” for the helicopter’s time and “t - 2” for the fighter’s time, because it waited around for two hours while the helicopter got a head start. Our table now looks like this.
Now, in order to complete the table, we need to use the formula, distance equals rate times time. This means we have to multiply across the rows of our table.
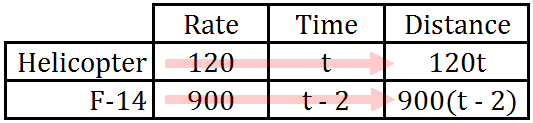
When the fighter finally catches up to the helicopter, they will be zero feet apart. In other words, the distance they travel will be equal to each other. So, we need to set their distances equal to each other and solve.
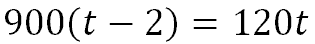
First, we do the distributive property.
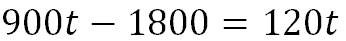
Next, we subtract 900t from both sides.
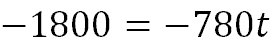
Finally, we divide both sides by -780.
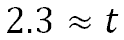
This means it will take approximately 2.3 hours for the fighter to catch up with the traveling helicopter. As a side note, 0.3 hours can be changed into minutes by multiplying it by 60, which is 18. This means it will take 2 hours and 18 minutes.
Example 2: “Maria left Juan's apartment at 5:00 pm. Juan came home and read a note, that detailed the route she was taking. If Juan leaves his apartment at 6:00 pm and follows the exact same route, when will Juan reach her if he is traveling at 15 mph and Maria is traveling at 10 mph?" We will employ the use of the table again.
We need to put in some details, like their rates.

Juan left 1 hour after Maria; so, we need to adjust his time. We will give Maria a "t" for time and we will give Juan a "t - 1" for time because he will be traveling 1 hour less than Maria.
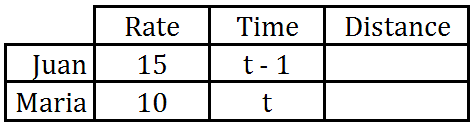
Now, we will multiply rate times time to get distance.
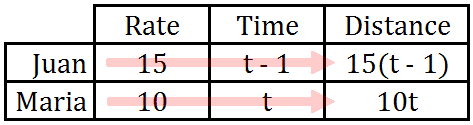
Just like example 1 above, when Maria and Juan meet, their distance will be equal to each other. So, we will set their distances equal to each other like so.
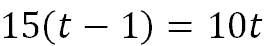
First, we need to do the distributive property.
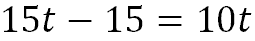
Next, we will subtract 15t from both sides.
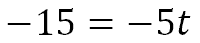
Last, we need to divide both sides by -5.
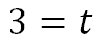
This means it will take Juan 3 hours from the time he leaves. Since he left at 6:00 pm, he will reach Maria 3 hours later, which will be at 9:00 pm. Now, try our video to gain deeper understanding and our quizmaster to check for understanding.
| |
Try our interactive quizzes to determine if you understand the lessons above.
This quizmaster uses distance, rate, and time along with rational expressions. For that reason, it is a difficult problem. | |
Try these lessons, which are closely related to the lessons above.
| |
 uiz:
uiz:  ideo:
ideo:  esson:
esson: