Solving Linear Equations | ||
| ||
Introduction | ||
In this lesson, you will learn how to solve linear equations. Here are the sections within this lesson:
|
ax + b = c | |
When solving linear equations of this form, we must carefully simplify the equation using a special two-step order. The term that is either adding to or subtracting from the variable must be canceled first by doing the opposite, otherwise known as the inverse operation. Let's take a look at this example.
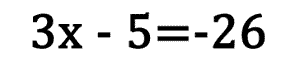 To solve for "x," we have to do the reverse order of operations. The subtraction by five can be undone by doing the opposite. We must add five to both sides.
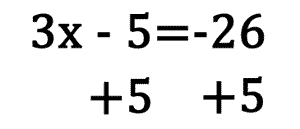 This simplifies accordingly.
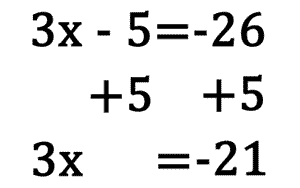 The next step involves cancelling the number next to the variable, and that number is called the coefficient. If the variable is being multiplied by a number, then we divide both sides of the equation by that number. If the variable is being divided by a number, then we multiply both sides of the equation by that number. Performing this step allows us to cancel the coefficient. In order to finish up our example, let's perform the last step. We must divide both sides by 3.
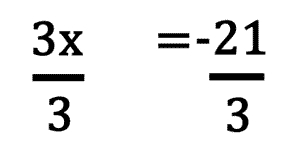 The solution is...
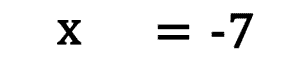 A nice fact about solving linear equations is that the solutions can be checked. The numeric solution is substituted into the original problem. Then the order of operations is used to simplify the remaining solution. Once simplified, both sides of the remaining equation should be equal to each other if the original answer is correct. Using our example above, we can see that our solution, x = -7 is correct because it checks. Substituting it into the original equation yields...
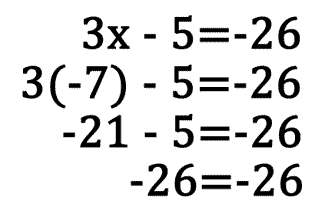 Here is another example. -4x + 1 = 21. First we must cancel the addition by 1 by subtracting 1 from both sides. Next, divide both sides by -4. This allows us to get the solution, x = -5.
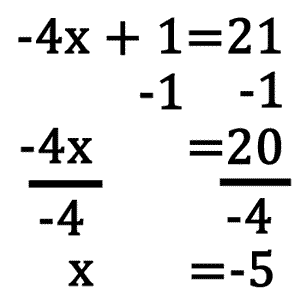 Upon checking we can see that -4 times -5 plus 1 is in fact 21. Therefore, x = -5 is the correct solution.
| |
ax + b + cx = d | |
This type of three-step linear equation must be simplified in order for it to be solved. In fact, we can simplify this type of equation into a two-step equation like the type mentioned in the previous section above. To solve these equations we must combine like terms. The terms that have the exact same variables are called like and can be combined. All we need to do is combine the numbers in front of the variables. For instance, let's examine this example.
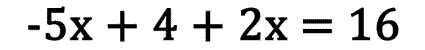 Notice that the left side has like terms. Those x-terms can be combined, as demonstrated here.
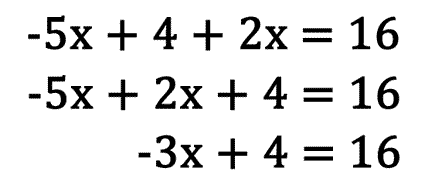
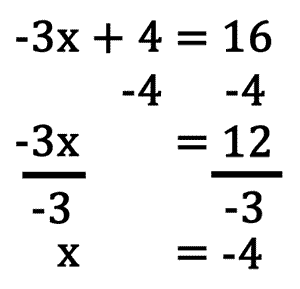 The final solution can be checked by substututing it within the original equation wherever the variable is located. Each variable must be replaced with the solution and the order of operations must be used to simplify the expression, similar to the steps used for solving two-step equations. Substituting the solution, x = -4 into the original equation yields the following.
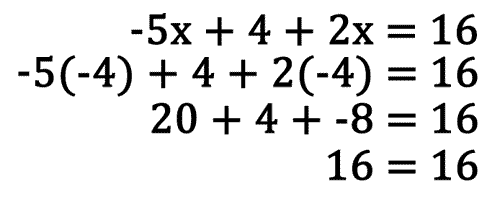 Since both sides of the final, most simplified line, yields the same value, this verifies that x = -4 is a correct solution.
| |
ax + b = cx + d | |
This is another type of linear equation that can be simplified in such a way that it can be transformed into a two-step equation. The procedure is similar to that mentioned immediately above, under solving three-step type 1 equations, but with a slight twist. Let's use this example.
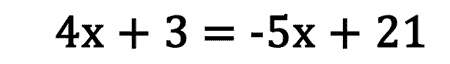 Equations of this type have like terms too but these terms are on opposite sides of the equal sign. In order to combine them, we must target one of the variable terms and add its opposite to both sides of the equation. This will cancel a term from one side and make the equation into a two-step equation. Let's cancel the -5x within our example by adding 5x to both sides of the equation.
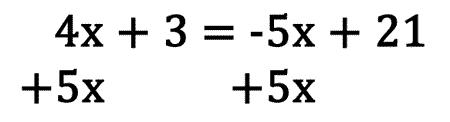 Now we can combine the x-terms, 4x and 5x. Simplifying, we get a two-step equation.
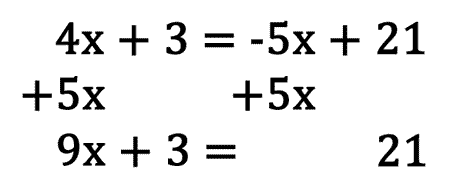 Solving the rest of the problem can be done following the procedure mentioned under solving two-step equations. A summary is provided below.
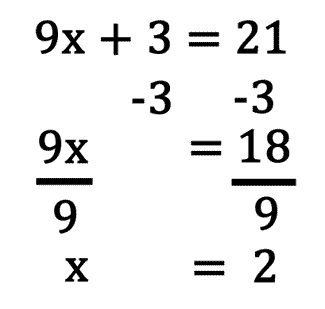 Checking the solution can be done by substituting the solution into the original problem for all the x-values.
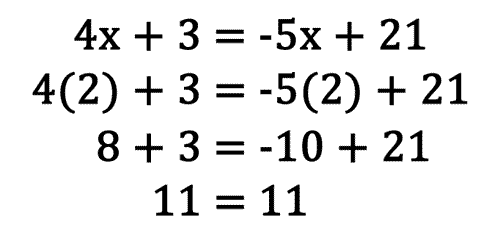 Since both sides of the equation simplify to the same value, this verifies that the solution x = 2 is the correct solution.
| |
After reading the lessons, try watching an instructional video.
|
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
|
View related MATHguide lessons.
|
 ideo:
ideo:  uizmaster:
uizmaster:  esson:
esson: