Pythagorean Theorem | |||
| |||
Introduction | |||
The Pythagorean Theorem is a mathematical relationship between the sides of a right triangle. A right triangle is any triangle that has one right internal angle. Pythagoras stated, if the length of the legs (smallest side) are squared and their sum is found, the sum will be equal to the square of the hypotenuse (longest side). Algebraically speaking, the relationship looks like...
The legs are traditionally marked with an 'a' and a 'b,' while the hypotenuse is marked with a 'c.' If that is the case, then the formula is a2 + b2 = c2. The next section will explain how the equation can be derived. | |||
The derivation of the algebraic relationship is also not very complicated, as far as most derivations go.
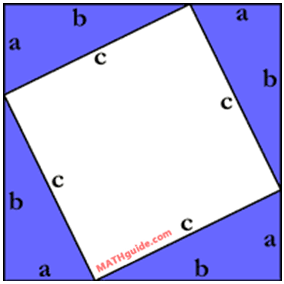
To derive it, we will examine the diagram below. The diagram consists of many simple figures. There is a white rotated square at the center. There are four blue right triangles. The entire figure, the rotated square and the four right triangles, is a large square, too.
The following explanation requires knowledge of area. Specifically, the areas of rectangles and triangles must be known to understand the explanation. Review the areas of the two figures before progressing.
The area of the inner white square is: A = (c)(c) = c2. The area of one blue right triangle is: A = (a)(b)÷2 = 0.5ab. The area of the entire square, which includes the white rotated square and the blue right triangles, is: A = (a+b)2. The derivation below begins with these areas in step one.
This means: "the sum of the squares of the legs of a right triangle is equal to the square of the hypotenuse." Watch our video that fully explains this proof of The Pythagorean Theorem.
You may want to use these activities that scaffold a step-by-step process for proving the Pythagorean Theorem.
The sections below will indicate how to use the relationship for two situations. One section tell us how to find a missing hypotenuse and the other a missing leg.
| |||
This section will explain how to use The Pythagorean Theorem to find a missing hypotenuse. If we are given a triangle's legs, then we would use the equation to calculate the length of the hypotenuse. Say we know the shortest sides to be 3 m and 7 m. The example below outlines the process by which we can calculate the hypotenuse.
Since our final value for c is 7.62, it means that the hypotenuse is 7.62 m in length. It also means we are done with the example.
| |||
This section will explain how to use The Pythagorean Theorem to find a missing leg. If we are given a triangle's leg and hypotenuse, then we would use the equation to calculate the length of the missing leg. Say we know the longest length to be 11 in and one of the other shorter sides to be 6 in. The example below outlines the process by which we can calculate the missing length.
Since our final value for a is 9.2, it means that the missing leg is 9.2 inches in length. It also means we are done with the example.
| |||
Watch these instructional videos.
|
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
|
You may want to use this activity that scaffolds the step-by-step process for proving the Pythagorean Theorem.
|
Here are lessons related to the Pythagorean Theorem.
|


 ideo:
ideo:  ctivity:
ctivity: 
 uizmaster:
uizmaster: 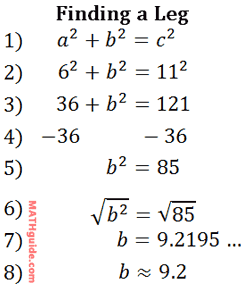
 esson:
esson: