Diagonal Length of a Cube | ||
| ||
Introduction | ||
This lesson will inform you how to calculate the length of a diagonal of a cube. Here are the sections within this lesson page:
If you are not familiar with the Pythagorean Theorem, it is strongly recommended you review our lesson on it before proceeding.
|
There are two different diagonals of a cube. Here is a view of them, side by side.
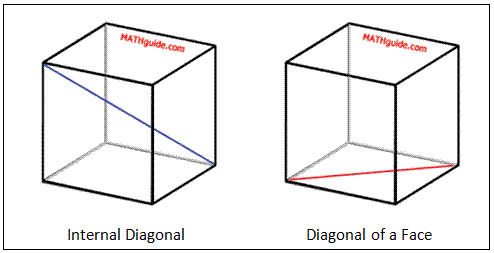
It can be seen the two are very different. The internal diagonal (marked dark blue) starts at one vertex and extends until it meets an opposite vertex, so that the segment exists entirely inside the cube. The diagonal of a face (marked red) starts at a vertex and ends at another vertex so that the segment exists entirely on a face of the cube. To calculate the diagonal of a face requires use of the Pythagorean Theorem, once. However, to calculate the internal diagonal of a cube requires use of the Pythagorean Theorem, twice.
These calculations will be shown in the next section.
| |
To calculate the internal diagonal of a cube, we must carry out several steps. Those steps will be explained within an example. Example: Determine the diagonal length of a cube that has an edge 5 feet long. Our first step is to calculate the diagonal of a face, shown below as a red segment.
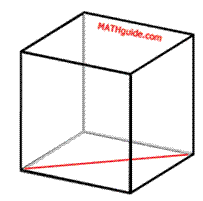
To determine this red length, we have to find the diagonal distance across a square. [All the faces are squares because the solid is a cube. Once a diagonal is drawn on a face, two congruent right trianges are created.]
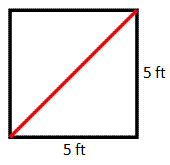
To find this distance, we must use the Pythagorean Theorem. If we let the red diagonal be represented with a 'c,' the mathematics looks like this.
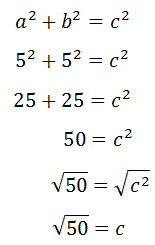
Next, we should examine the internal diagonal (marked blue) of the cube in relation to the diagonal of the face (marked red), below.
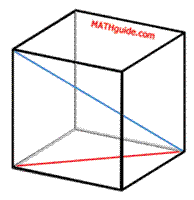
To calculate the length of the internal diagonal, we need to use another right triangle. We will use the edge of the cube as a leg, the diagonal of the face as another leg, and the internal diagonal as a hypotenuse. Here is that right triangle with its dimensions.
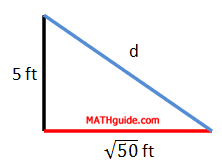
Again, we have to utilize the Pythagorean Theorem to solve for the internal diagonal, which has been marked with a 'd' above.
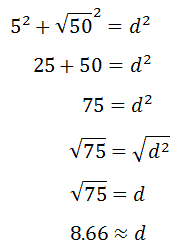
Therefore, the length of the internal diagonal is approximately 8.66 feet in length.
| |
Try this instructional video. | |
Try this interactive quiz.
| |
Try this lesson, which is related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: