Mixture Word Problems | ||
| ||
Introduction | ||
Here are the sections within this lesson:
|
We live in a world where industries create a variety of products. Engineers use concrete and metals to build structures. Food companies, with the help of chemists, farmers, nutritionists, and botanists, combine a multitude of ingredients to make delicious edibles. Textile manufacturers use a variety of materials, both organic and synthetic, to weave new designs for clothing. When concrete, foods like (trail mixes), and textiles are mixed, it is necessary to discuss weights, costs, volumes, masses, and other parameters. The weight/item, cost/pound, volume/item, or mass per unit of volume are some of the characteristics that are important as art of the process.
The lessons below will teach you how to mix items that have different costs using a food environment. However, the units could easily be changed to account for other characteristics for other industries.
| |
To delve deep into the world of mixtures, we need to know some basics. Consider this problem. Example 1: How much would it cost to purchase 30 pounds of crackers if they cost $2/pound? Consider multiplying those values, like so.
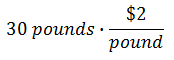
We could place the 30 pounds over one, essentially creating a fraction.
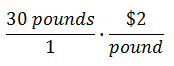
Now that we are multiplying two fractions, we can cancel factors on the top and the bottom that are the same. The pound units cancel:
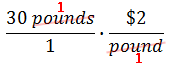
Now we multiply across to get:
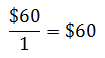
If we keep in mind that we multiplied a volume times a cost, this extremely basic mixture problem leads us to a formula.

If for some reason we are calculating cost based on volume, the formula would be slightly different. Example 2: If soil costs $125 per cubic yard, how much would 3 cubic yards cost? To answer this question we must use this new formula.
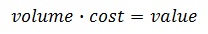
So, we will plug in what we know inside the new formula and perform a similar set of calculations like we did for our first example above.
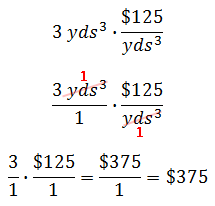
These formulas will enable us to do a variety of more complicated mixture problems.
| |
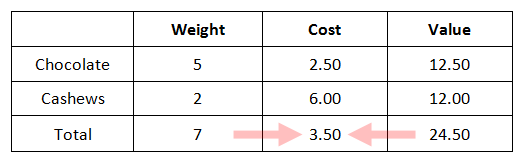
In the last section, we saw how to calculate the value of a product given its cost and either its volume or its weight. Now we will examine a case when we mix two substances together and determine the combined unit cost. Example: A local grocery store mixed 5 pounds of chocolate with 2 pounds of cashews to create their own bars of chocolate. If the chocolate costs $2.50/lb and the cashews cost $6/lb, how much will the new mixture cost per pound? This problem requires a great deal of organization. To assist in the organization process, we can use this table.
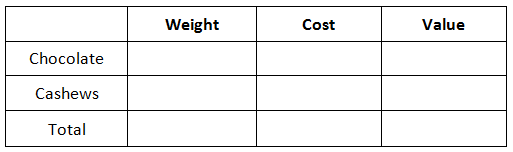
Notice how the columns list weight, cost, and value in that order. This order is helpful because we can multiply weight times cost to obtain value. We were given four quantities. Let us start to place them inside the table. For instance, placing the costs in their appropriate locations is the first step, like so.
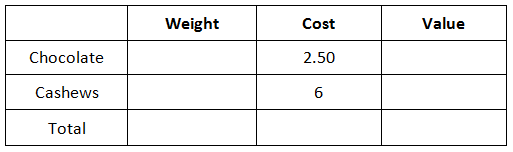
Now, we can place in the 5 pounds of chocolate and the 2 pounds of cashews within their respective locations, like so.
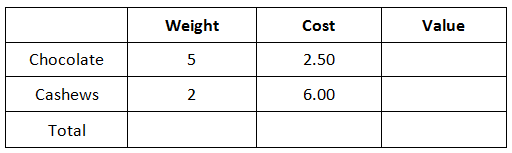
It can be seen that all of our given information is within the table. Now, we will multiply across the table, since weight times cost equals value.
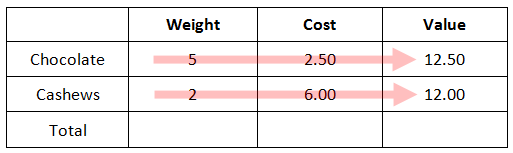
We can also add the quantities within the first and last columns to find the total weight and the total value of the mixture, like so.
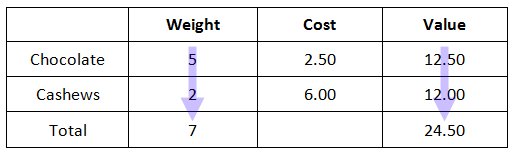
Our last step requires one final calculation. Since we are required to calculate the cost of the mixture per pound, we have to manipulate the equation surrounding this relationship. Recall the formula.

If we divide each side by weight to solve for cost, we get these steps.
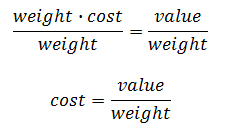
So, we will divide 24.50 by 7 to get the solution.
Would you like to see our instructional video on intermediate mixture problems? Here it is.
To determine if you truly understand this lesson and the video, try our quizmaster below. | |
The Intermediate Mixture Problems lesson informed us how to determine the cost when we mix items that have different costs. For this lesson, we will be given a supply of two ingredients that have different costs and we will calculate how much of each we will need to gain a mixture that has a specified cost. Here is a problem. Example: Mrs. Harkins wants to make 50 pounds of brownies that costs $3/pound. She will be combining a $3.50/pound brownie mix and $1/pound mini-marshmallows. How many pounds of the brownie mix and how many pounds of the marshmallows does she need to use? Just like the previous unit, we need to use a table to organize our information. Let us start by placing the information from our first sentence into a table. The quantities refer to what Mrs. Harkins wants to make, which is our total mix.
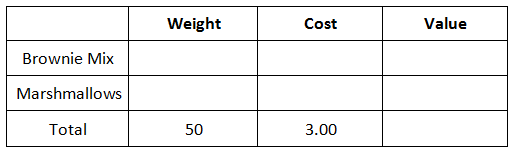
Now, we need to move on to the next sentence, which are the costs for the brownie mix and the marshmallows.
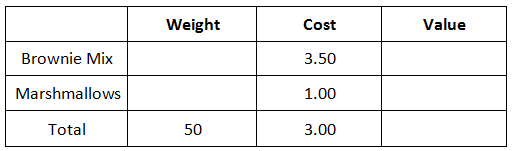
We are ow done entering in our given information. We have to be a little creative to continue solving this problem, which means we have to use algebra. We currently do not know how many pounds of brownie mix and marshmallows to use. However, we will use an x-value and a y-value to represent their weights, respectively. We need to place those letters into the table.
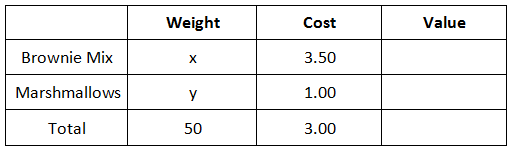
We can calculate the last column simply by multiplying from left to right. Why? It is because weight times cost equates to value. Here is the last column of values.
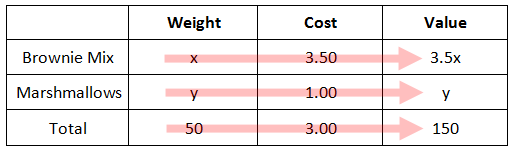
Our next step is now to look at this vertically. We know that the total weight is gained by adding the weight of the brownie mix and the marshmallow mix. We also know that the total value is obtained by adding the values for the brownie mix and the marshmallows.
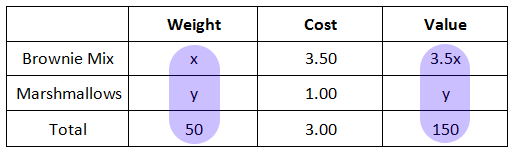
This leads to two equations.
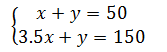
To solve this system of equations, we can use a variety of techniques [see our lessons on Systems of Equations]. The work for solving the system of equations will not be shown here. Nevertheless, the solution is (40,10). The x-value stands for the weight of the brownie mix and the y-value stands for the weight of the marshmallows. This means Mrs. Harkins has to use 40 pounds of brownie mix and 10 pounds of marshmallows. Watch a MATHguide video to digest this skill.
Try our quizmaster to see if you can solve your own problem. | |
Here are videos for mixture problems.
| |
Here are quizzes that are related to the lessons above.
| |
Try this lesson, which is closely related to the lesson above.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: