This lesson page will inform you how to evaluate a cetain limit that involves the sine function. Here are the sections within this lesson page:

• The Sinusoid Problem
• Degenerative Problem 1
• Degenerative Problem 2
• The General Case
• Specific Example of the General Case
• Interactive Quizmasters
• Related Lessons

    The study of limits involves a variety of functions, like logarithmic, exponential, rational, and trigonometric to name a few. This lesson will examine a specific type of limit. This one:

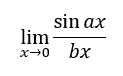
    To solve the type of problem mentioned in the previous section, we need to look at a simpler problem, namely:

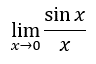
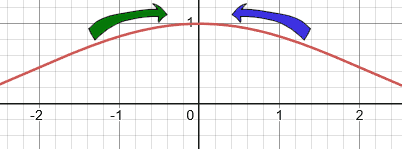
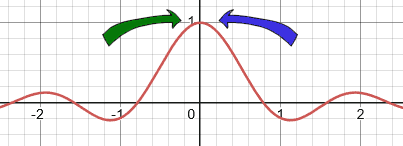
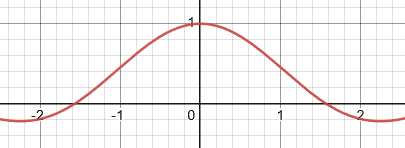
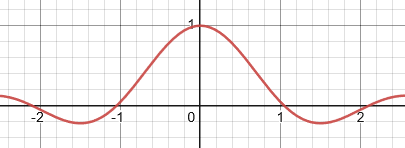
    To determine this limit, we can use a graphical approach. Here is the graph of...

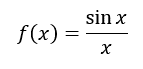
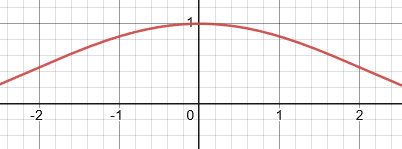
    To determine the limit, we have to look at both sides of zero because we are looking at y-values as the function approaches x = 0.

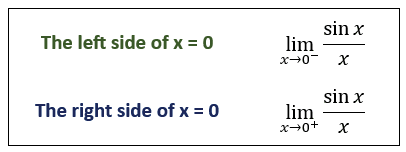
    Both the left side and the right side of x = 0 approach the same y-value. The y-value is 1.

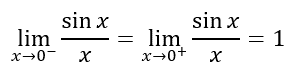
    We can now move to a broader problem, based in part on the findings from the last section. Look at this problem:

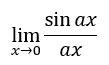
...where the a-value is never zero. This encompasses an entire problem class. Surprisingly, as the a-value changes, something stays the same.

    We already saw the case for the a-value being equal to one. Let us examine when the a-value changes by looking at their corresponding graphs.

a-value = 1
a-value = 2
a-value = 3

    All of the graphs have the same limits left and right of zero. Take for instance the case where the a-value is 4. Look at the left and the right limits.

    This tells us when the a-value is not zero...

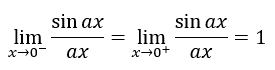
    Which means...

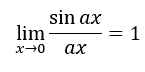
    The conclusion within the last section gave us a great gift of knowledge for dealing with a harder type of problem, but what if the coefficients were not equal?

    Here is the general case:

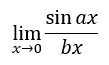
    To solve this, we have to realize that the coefficient in the numerator is the driving force that will propel us forward. So, we will multiply the top of the fraction and the bottom of the fraction by the a-value, which is permitted for our fraction since the a-value is not equal to zero.

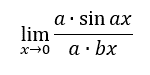
    We can multiply in any order, so we can switch the order of multiplication in the denominator.

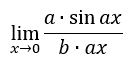
    Now, we need to be creative with our representation of the problem by separating the fraction into a product of two fractions.

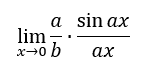
    Constants do not affect limits, which gives us this.

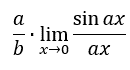
    We already know the value of that limit. We know it is equal to one.

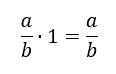
    By using several logical steps, we now know this to be true.

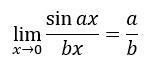
    After seeing how to solve the general case, you can determine if you understand the lesson by trying a specific case with the quizmaster below.

    uiz: Sine Coefficient Limit Problem

    Be aware, you will likely not be allowed to take a short cut. For instance, you will have to show work to solve a problem like the one below.

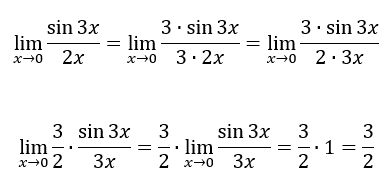
    Use the following quizmaster to determine if you understand the lesson above.

    uiz: Sine Coefficient Limit Problem

    Try this interactive quizmaster to determine if you understand frequency tables.

    uiz: Sine Coefficient Limit Problem

    Try this related material.

    esson: Limits of Ratios of Polynomials
    esson: Limits by Factoring
    esson: Limits of Piecewise Functions
    esson: Limits: Numerical Approach
    esson: Limits by Conjugates