Limits: by Factoring | ||
| ||
Introduction | ||
This lesson page will inform you how to find limits of certain rational functions using polynomial factors. Here are the sections within this page: If your factoring and reducing of rational expression skills need assistance, review these lessons before proceeding.
|
For some limits, the problem can be solved using substitution. Here is an example of such a limit.
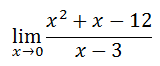
We need only replace the xís with 0, like so.
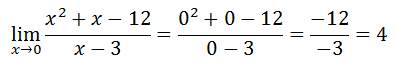
Here are two more examples.
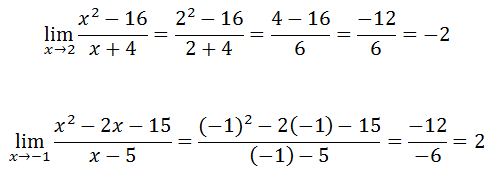
However, not all problems are so simple. The next section will show how substitution alone is not always a reliable technique for calculating a limit.
| |
In the last section, we saw how we could use substitution for this problem.
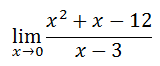
Now, letís see what happens if we use substitution as we approach x = 3 instead of x = 0.
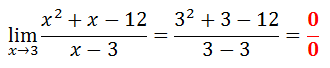
This is a call for mathematical alarm because the denominator cannot be equal to zero. Why? This video explains why division by zero is illogical. https://www.youtube.com/watch?v=3hkFl4yYM_I Anytime we substitute a value into a function and get a denominator equal to zero, we get an undetermined result. It means the process tells us absolutely nothing about the limit. It also means we have to try some other strategy. The other strategy is to factor the polynomial. If we factor the function, we can reduce the rational function, like so.
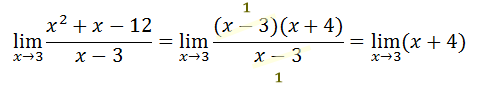
Now we can use substitution because we no longer get a zero in the denominator when we do so.
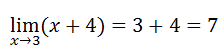
Here are two more examples using factoring as a strategy.
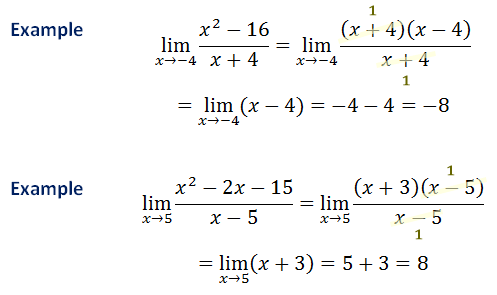
| |
Try this instructional video to learn this lesson.
| |
Try this interactive quizmaster to determine if you understand the lesson.
| |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: