Solving Trigonometric Equations | ||
| ||
Introduction | ||
In this section, you will learn how to solve trigonometric equations. Here are the sections within this lesson:
|
Learning how to solve trigonometric equations requires a lot of prerequisite knowledge. It is strongly suggested that you first be knowledgeable with these lessons before progressing to the lessons in the next sections:
| |
This video will explain how to solve basic trigonometric equations. | |
This video will explain how to solve more involved trigonometric equations that require more algebra. | |
This video will explain how to solve trigonometric equations using a graphing calculator. As aside note, the method used within this lesson is not unique to trigonometric equations. This method can be used on any equation that can be graphed on a graphing calculator, which can include non-functions (see polar equations). To demonstrate how to use a graphing calculator as a strategy, let's look at a problem. Example: Solve the trigonometric equation sin2 x + 0.5 = 3cosx on the interval [0, 2π). For the purposes of this problem, a TI-Nspire is being used. First, make sure the calculator is set in radians. We have to use radians because the interval is set in radians. We then graph each side of the equation separately. Looking at the picture below, you will see the left side of the equation is in blue and the right side is in red.
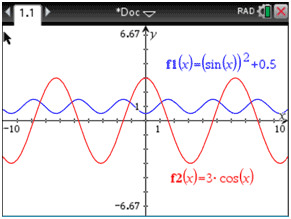
Next, find the intersections between [0, 2π), which means [0, 6.28) approximately. For the TI-Nspire, use this: Menu :: Windows :: Analyze Graph :: Intersection.
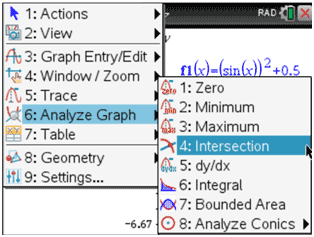
Here is the result on the graph.
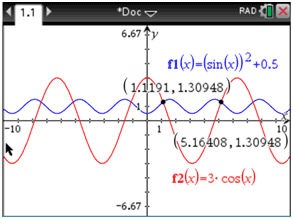
Since the original equation contained x-values, the solutions to the equation are x-values only. So, the solution set is {1.119, 5.164}. You may be wondering, “Why aren’t the other intersections solutions of this equation?”
If there was no interval to which we were bound, we could provide an infinite number of solutions. However, we are only allowed to report the intersections that occur between x > 0 and x < 2π (which is approximately 6.28).
| |
Try our instructional videos to help learn this material.
| |
Try these lessons, which are closely related to the lessons above.
| |
 esson:
esson:  ideo:
ideo: