Solving Radical Equations | ||
| ||
Introduction | ||
This lesson page will inform you how to solve radical equations. Here are the sections within this lesson page:
|
Let us look at a simple problem, like this radical expression and its equivalent form.
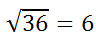
To prove that the equivalent form is 6, we need to check by multiplying the answer by itself.
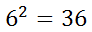
Since 6-squared is 36, the square root of 36 is 6. This means square roots and squares are inverse operations. Similarly, cube roots and cubes are inverse operations, and so on. Likewise, we can deal with expressions that contain only variables, like this one.
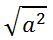
To fully understand this, we can use our knowledge of Power Rules for Exponents, namely the Fractional Exponents lesson. We can write our expression, like so.
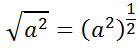
This is because a square root is really a half power. Continuing on, using the Power to a Power to a Power rule, we get...
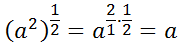
Again, it becomes clear that square roots and squares are inverse functions.
We will make use of these inverse functions in the sections that follow.
| |
We will look at a few simple radical equations to get a feel for the logic and the process we need to use to solve them. Before we get started looking at examples, it should be known that there is an important first few steps when solving radical equations. This graphic summarizes those steps.

Example 1:
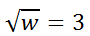
The strategy for dealing with radicals is the same for all problems and it is worth emphasizing throughout this lesson; GET THE RADICAL ALONE. Well, it's already alone on one side of the equation. The next step is to: DO THE INVERSE OF THE RADICAL. The inverse of square rooting is squaring. So, we need to square the square root. Whatever we do to one side of an equation, we need to do to the other side, like so.
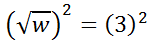
Now, let's simplify both sides.
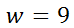
Before we celebrate too early with our solution, we should check it within the original equation to see if it truly is a solution. [This step is important, especially in later sections of this lesson.] Here is the checking process.
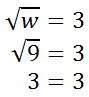
Since both sides are equivalent, w = 9 is a solution. Example 2:
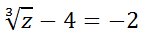
To solve this equation, we have to first get the radical alone. So, we need to target the subtraction by four.
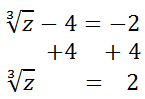
Now, we need to do the inverse of the cube root, which is cubing.
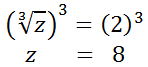
The next step is to check the solution within the original equation.
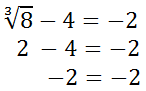
We have a truthful statement. This shows that z = 8 is the correct solution.
| |
This section will deal with slightly more complex equations. Example:
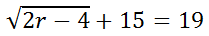
This problem has a few more steps. Let's start by getting the radical alone by targeting the 15.
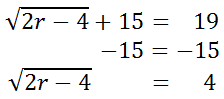
Now, we need to "cancel" the radical by doing the inverse operation.
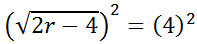
We get this.
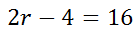
Next, we solve for 'r' using algebra.
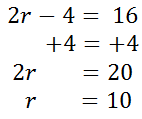
We need to check the value r = 10 in the original equation.
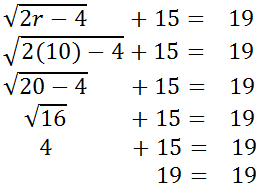
This is true and it confirms r = 10 is the correct solution. Try this video and interactive quizzes. They will help you learn the lesson.
| |
Before attempting to understand this section, you must have some knowledge of other topics in mathematics. If these topics are unknown to you, please review them before continuing.
Here is an example of an advanced radical equation. Example:
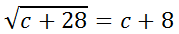
Since the radical is already alone on one side of the equation, we can take care of the square root by squaring both sides.
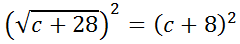
The square root and the square are inverse operations, so they "cancel" each other. However, the right side involves multiplying a binomial times itself. We need a table to do that -- see our lesson on the topic, called Operations on Polynomials: Multiplication. Here is a table that shows the multiplication that occurs on the right side.
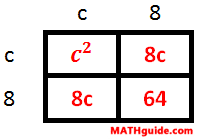
This leaves us with this equation.
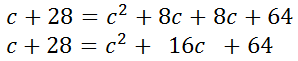
To solve this remaining quadratic equation, we have to get a zero on one side of the equation. [If you need to familiarize yourself with quadratic (degree two) equations, see several of our related lesson: Solving Quadratic Equations.]
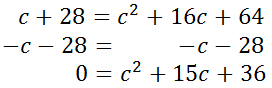
Now that we have a zero on one side of the equation, we can choose from several techniques to solve the quadratic equation: factoring, utilizing the quadratic formula, completing the square, graphing, and using the calculation ability of a modern calculator. By looking at this equation, we can see that it is factorable.
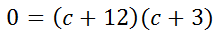
Continuing, we get...
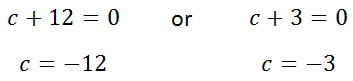
Last, we have to check these values in the original equation to determine if they are actual solutions. Here are the details of that check.

Try this instructional video and interactive quiz. They will help you learn the lesson.
| |
Try these videos, which can help you learn the content above.
| |
Try these quizzes, which can help you learn the content above.
| |
Try these lessons, which are related to the sections above.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: