Simplifying Radicals | ||
| ||
Introduction | ||
This lesson page will inform you how to solve radical equations. Here are the sections within this lesson page:
To understand how to simplify radical expressions, we have to factorize numbers. Please review this lesson before proceeding if your knowledge of identifying factors needs help.
|
When we simplify square roots, it is important to understand the fundamentals using the basics. What is this expression equal to?
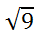
It is equal to 3, but why? Here is the reason.
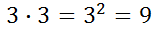
So, we can see squaring is an inverse operation with square roots. Similarly, look at this problem with a cube root.
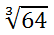
The answer is 4. Here is the reason.
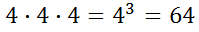
It is evident that cubing and cube rooting are inverse operations.
| |
Radicals have several parts. Let us review the parts of a radical expression.
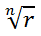
The symbol that looks like a checkmark is called a radical. A number under the radical, marked with the letter 'r,' refers to the radicand. The small number written by the checkmark, marked with the letter 'n,' refers to the index. If an index is not written, it is assumed to be a 2 and is a square root radical.
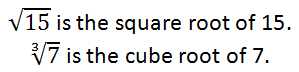
| |
To simplify radical expressions, here are the steps within this graphic organizer:

| |
The best way to learn how to simplify an expression is to examine an example. Example 1:
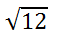
This problem does not have a perfect answer. If we were to use a calculator to find the solution, it would provide us with a decimal solution somewhere between 3 and 4. Our only other option is to simplify the radical using the steps outlined within our graphic organizer in the last section, Steps for Simplifying Radical Expressions. We will begin with a factor tree. We will break up the 12 as 3 times 4.
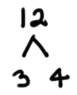
If a prime number is found, circle it. 3 is prime because it has no other smaller factors other than 1. However, 4 is not prime (called composite) and it can be factored as follows.
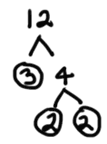
So, we will write these in place of the 12 under the radical.
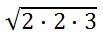
Since the index is not written, it is 2. This means we group the factors in groups of two, like so.

For each group, a factor comes out. Anything ungrouped will remain under the radical, like so.
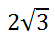
Example 2:
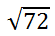
This is a factor tree for the radicand 72.
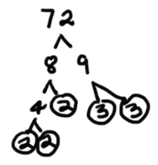
Now, we will write the prime factors under a radical.
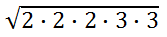
The next step is to group the factors. The index is 2, so we will group in pairs.

Place a factor on the outside of the radical for each group.
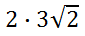
Next, clean up the problem to get the final answer.
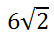
Go to the next section to see examples with cube roots.
| |
Here are some examples that contain numbers and variables. Example 1:
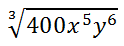
The factor tree is not shown, but here are the factors of 400.
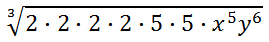
Let us also write all the factors of the letters.
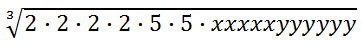
We will now use the index 3 to remind us to group the factors by triples, like so.

For each group, place one factor outside of the radical. All ungrouped factors remain inside the radical.
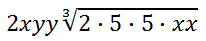
Multiplying the factors to clean up the expression, we get...
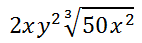
Clearly, we can see that the variables add no more complexity to simplifying radical expressions.
Example 2:

First, write the prime factors of the radicand.
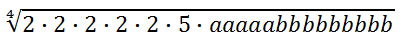
Next, group the factors by quadruplets because the index is 4.

Next, place a factor outside the radical for each group. Ungrouped factors remain inside the radical.
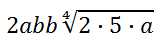
Now, we need to clean up the problem for the final solution.
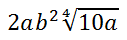
| |
Try these videos, which can help you learn the content above.
| |
Try this quiz, which can help you learn the content above. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: