Margin of Error & Confidence Intervals by Formula | ||
| ||
Introduction | ||
Margin of error is the quantification of inaccuracy that is built in to the data gathering process. It is an important consideration when reporting or deciphering information. This lesson will inform you how to calculate margin of error (and confidence intervals) by using formulas. Here are the sections within this lesson page:
|
This sections that follow require a basic understanding of statistics. If you are not familiar with margin of error and confidence intervals, please review this lesson before proceeding. | |
Here are the formulas for a margin of error when calculating a 95% confidence interval.

The p-hat is the proportion and again the n-value is the number of data points we have.
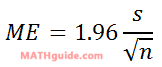
The s-value is the sample standard deviation. The n-value is the number of data points we have.
These formulas can be adapted for different confidence levels (other than 95% confidence intervals). However, doing so is an advanced topic for another time that involves understanding z-values to modify the 1.96 coefficient.
| |
The best way to understand how to use the formula is by looking at an example. Example: A certain poll says 35% of registered voters favor Mr. Dimos in the upcoming senate race. If 600 people were polled, determine a 95% confidence interval for this poll result. First, we need to identify the values we were given. The 35% is the p-hat (the proportion). The 600 is the n-value. Now, we can plug this information into the formula.
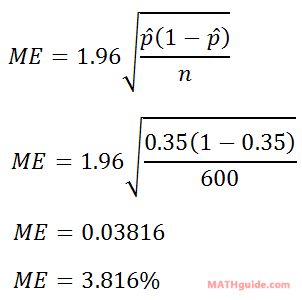
We can take this margin of error and we can build our confidence interval, like so.
High End: 35% + 3.82% = 38.82% So, the confidence interval is…
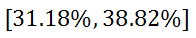
This confidence interval means: If another poll was taken again, the mean of the data would be 95% likely to fall between 31.18% and 38.82%.
| |
If given a list of data from a survey, experiment, or some other activity, we will use a different formula for determining the margin of error. We will look at a specific example to see how this formula is used. Example: Sentences were chosen at random from Michael Medved's book The American Miracle: Divine Providence in the Rise of the Republic. The number of words in the sentences were counted. This is the result.
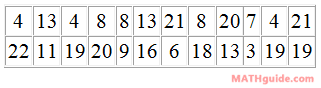
Use the data above to: a) determine the mean and sample standard deviation, b) calculate a 95% margin of error, c) determine the respective confidence interval. Whether by hand or by calculator, the sample standard deviation must be determined. The result is 6.496, rounded to the nearest thousandth. Now, we can use the formula to calculate the margin of error. We will plug in the sample standard deviation (s), which is 6.496. The n-value is the number of data points and in this case it is 24 (see the 24 data points in the table). Here is the information entered into the formula.
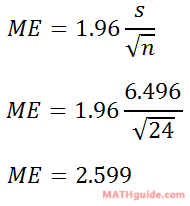
The mean of the data, which was collected by calculator, is 12.75. Now, we can determine the confidence interval.
High End: 12.75 + 2.599 = 15.349 So, the confidence interval for this data is…
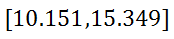
This means if a random sample of sentences were to be taken from the same book, there is a 95% probability the mean of the data would fall within 10.151 and 15.349 words. | |
Try this video, which can help you learn the content above.
| |
Try this quiz, which can help you learn the content above.
| |
Try this activity. It helps students use a MATHguide instructional video to learn how to use a formula to determine a confidence interval. It addresses Common Core State Standard HSS-IC.B.4. | |
Try these lessons and the quizmaster, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity: