Margin of Error & Confidence Intervals | ||
| ||
Introduction | ||
This lesson page will teach you about standard deviation. Here are the sections within this lesson page:
|
As important elections get closer (technically, all elections are important), statisticians go out and retrieve voter samples. They ask, “Who will you be voting for?” After tabulating the results of their sample, they then calculate the amount of error there is. How can there be error?
If all voters are not asked, it is impossible to be sure the survey is perfectly accurate. We call this uncertainty the margin of error. This will be explored to more detail in the following sections.
| |
Margin of error has several definitions. All of them provide insight to understanding margin of error.

| |
A random survey could tell us that 30% of the respondents favor Mr. Wowzer (a fictitious candidate) with a margin of error of 5%. What does this mean? To determine the interval of our survey, we add 30% and 5% to get the high end and we subtract 30% and 5% to get the low end. This means our high end is 35% (30% + 5%) and our low end is 25% (30% - 5%). We would write the interval as…
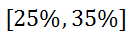
This tells us that the real number is actually somewhere between 25% and 35%. Here are two example problems. Example 1: A random survey says 47% of all respondents like watching the Oscars with a margin of error of 4%. Calculate the confidence interval for this statistic. Here is the math.
47% + 4% = 51% The confidence interval is…
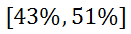
Example 2: Looking at a poll, we learn that 25% of all registered voters want to repair streets, but also do not want higher taxes. If the margin of error is 3.5%, calculate the confidence interval.
High: 25% + 3.5% = 28.5% The confidence interval is…
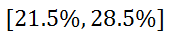
| |
It may be possible that we are given a confidence interval and have to determine the margin of error. Here are two examples for this situation. Example 1: The confidence interval for a survey is [22%,28%]. Determine the margin of error. The margin of error is always exactly between the high end and the low end of the confidence interval. So, one way to find the confidence interval is to find the mean of the interval. Here is the calculation.
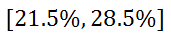
Example 2: If the confidence interval for a survey is [87.5%,93.5%], determine the margin of error. We can look at a different strategy than the strategy which was used in the last example. How far apart are the two numbers that define the interval? From 87.5% to 93.5%, we can subtract the two numbers.
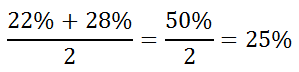
We know the mean of the survey sample rests exactly at the center of the interval or half the total length of the interval. This tells us the mean has to be 3% (half of 6%) units from either of the extremes. So, 87.5% + 3% = 93.5% - 3% = 90.5%. Since 90.5% is the mean of our survey, then the margin of error is 3% (half of the total length of our confidence interval). | |
Try this quiz, which can help you learn the content above.
| |
Try these lessons and the quizmaster, which are related to the sections above.
| |
 uiz:
uiz:  esson:
esson: