Completing the Square | ||
| ||
Introduction | ||
In this section, you will learn how to complete the square to solve quadratic equations. Here are the sections within this lesson:
|
Completing the square is a reference used to describe a technique for solving quadratic equations. There are several techniques for solving quadratics, like graphing and using the quadratic formula. This lesson will focus on only the completing the square technique. | ||
In order to understand this technique, one first needs to understand perfect square trinomials. To understand them, we need to look at a few problems. Letís square a binomial.
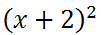
If you need to see how one multiplies binomials, review this lesson: Operations on Polynomials. Nevertheless, the answer is this.
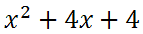
The trinomial above is called a perfect square trinomial because we obtained it by squaring a binomial. We will take a look at another.
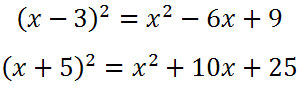
The trinomials on the right side of each equation are both perfect squares.
| ||
The central theme to the technique called, 'completing the square,' involves understanding several relationships. To gain insight to these relationships, we will look at a few perfect square situations with blanks. Here is one situation.
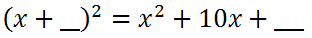
In order to make this (x + 5)2, the last blank has to be 25. However, we need to understand the relationship between the 10 and the 25. How can we mathematically manipulate the 10 to make it equal to 25? The relationship involves two steps:
Similarly, here is another problem.
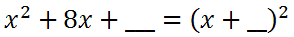
Take half of 8 to get 4. Square the 4 to get 16. This gives us...
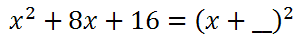
Factoring the trinomial gives us this final perfect square.
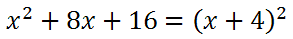
The number inside the parentheses, the 4, is always half of the middle term of the trinomial, which is the 8. Here are the relationships next to the trinomial and the perfect square.
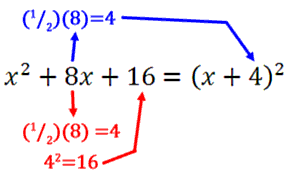
| ||
Here are two problems that will employ the technique by the same name to solve two quadratic equations.
Example 1:
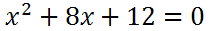
First, we will subtract 12 from both sides.
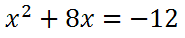
To progress using the 'complete the square' technique, we need to determine what to add to both sides to create a perfect square on the left side of the equation.
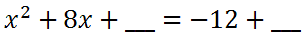
To determine this value, use this formula using the 8. Divide it by two, then square the value, like so.
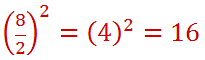
We will then add 16 to both sides of our equation.
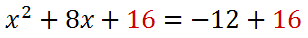
We created a perfect square trinomial on the left side of the equation. We will write it as a perfect square and also clean up the right side of the equation.
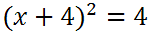
To cancel the square on the left side, we will take the square root of both sides. When we do so, we have to use a + on the right side.
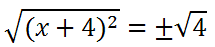
Both sides can be simplified. On the left side, the square and the square-root cancel each other. The square-root of 4 is 2. This is the result.
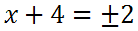
To solve for 'x,' we have to subtract 4 from both sides.
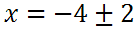
Here are the two solutions.
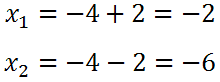
Sometimes the solution is written like this.
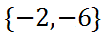
Do not misinterpret it as an ordered pair. Notice there are no parentheses. There are braces, instead.
| ||
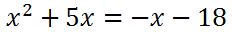
We need to get all the x-terms on one side. With that goal in mind, we need to add 'x' to both sides.
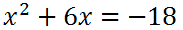
Next, we need to complete the square on the left side. To do so, we have to add a value to both sides.
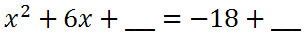
To determine what value to add, we have to use this formula. We have to divide the 6 by two and then square the result.
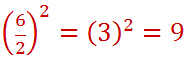
Therefore, we need to add 9 to both sides of our equation.
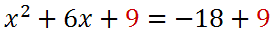
We will write the left side of the equation as a perfect square. We will also simplify the right side.
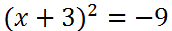
Now, we need to cancel the square by taking the square-root of both sides. We need to add a + sign to the right side, too.
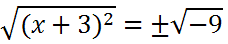
We will now clean up the left side by canceling the square and the square root, since they are inverse operators. As for the right side, the square-root of -9 is 3i.
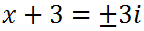
We will subtract 3 from both sides.
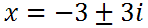
Here are the two solutions.
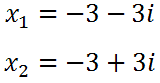
Sometimes the solution is written like this.
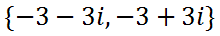
| ||
View our instructional video on the lesson above. | ||
Try our interactive quiz to determine if you understand the lessons above. | ||
Try these lessons, which are closely related to the lesson above.
| ||
 ideo:
ideo:  uiz:
uiz:  esson:
esson: