Using the Quadratic Formula | ||
| ||
Introduction | ||
This lesson will teach you how to solve quadratic equations by using the quadratic formula. Here are the sections within this lesson:
| ||
The quadratic equations that will be solved within this lesson will be second degree equations of a single variable. The equation must be of the form...
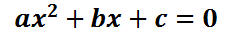 In other words, the equation must be equal to zero. Only then may we be able to identify the "a," the "b," and the "c" within the equation. The "a" is the coefficient of the squared term. The "b" is the coefficient of the linear term and the "c" is the constant term. When quadratics are in this form, they can be solved using this formula.
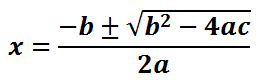
See our instructional videos section to see how the quadratic formula was derived.
| ||
Here is our first example of a quadratic equation.
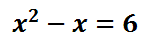 To get the equation equal to zero, subtract 6 from both sides. Doing so, we get...
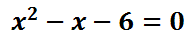 For this example, a = 1, b = -1, and c = -6. We will substitute these values into the formula.
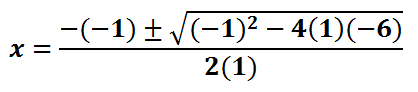 We can clean up the formula by taking the opposite of negative one and by cleaning up the expression underneath the radical. We can also simplify the denominator by multiplying two and one.
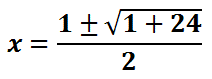 Simplifying further, we get...
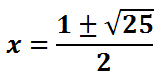 The square root of 25 is 5.
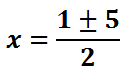 Once we get down to this step, we have to bifurcate (split into two). The "+" means we have two equations -- one equation with a plus and the other with a minus sign.
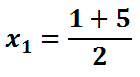 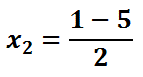 Now we will solve each separately.
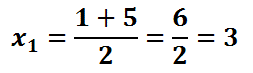
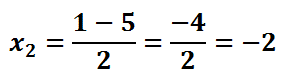
Therefore, the two solutions are 3 and -2.
| ||
However, not all equations are this simple to solve. Let us examine another example.
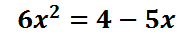 Again, we have to get the equation equal to zero before we use the quadratic equation. We must add 5x to both sides and subtract 4 from both sides to get zero on the right side.
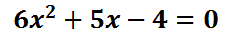 Now, a = 6, b = 5, and c = -4. These values must be substituted into the formula as follows.
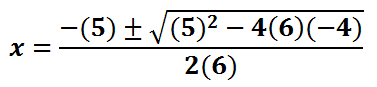 We can start cleaning up the formula.
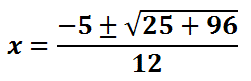 The value under the radical is 25 + 96, which is 121.
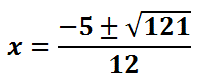 The square root of 121 is 11.
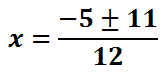 Now, we bifurcate and simplify.
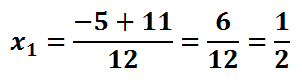
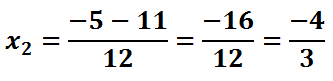 This makes the two solutions 1/2 and -4/3.
| ||
Watch our instructional videos:
| |
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
| |
 esson: Completing the Square esson: Completing the Square esson: Operations on Polynomials esson: Operations on Polynomials esson: Rational Expressions esson: Rational Expressions esson: Factoring esson: Factoring esson: Polynomials, Factors, Zeros esson: Polynomials, Factors, Zeros esson: Conic Sections esson: Conic Sections | |
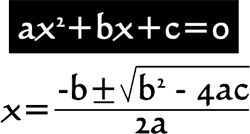
 ideo:
ideo:  uiz:
uiz: