Circles | ||
| ||
Introduction | ||
In this section, you will learn how to graph circles. Here is a list of the sections within this webpage:
|
The equation of a circle may look intimidating at first glance, but it is simple to use. Here is the equation.
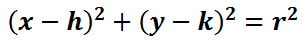 The 'h' and the 'k' relate to the center of the circle (h, k) and the 'r' stands for the radius of the circle. The radius is defined as the distance from the center to all points on the circle.
Another definition of a circle is the locus of points in a plane that are all a constant distance, called a radius, from a point, which is called a center.
| |
Now that we know what the equation of a circle looks like, let us use an example to see how to graph a specific equation. Here is an equation with specific values.
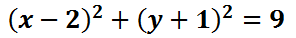 To locate the center, take the opposite of the values in the parentheses. The value next to the 'x' is the x-value of the center. The same is true for the value next to the 'y.'
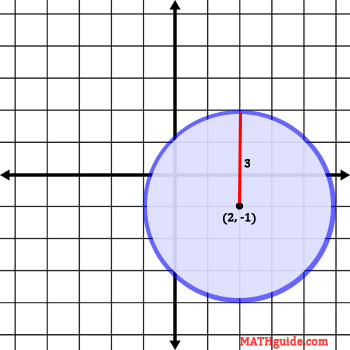
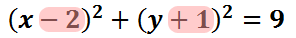 So, the center is at (2, -1). We will now graph the center with the circle and explain how it came to be.
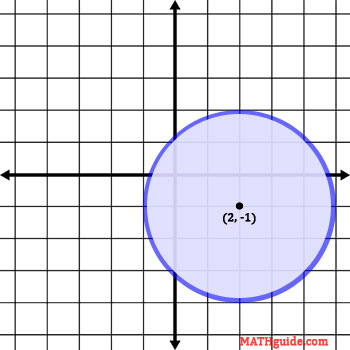 Now let's turn to the value on the right side of the equation.
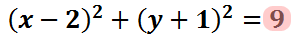 The right side of the equation is the square of the radius.
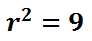 To obtain the radius, we take the square root of both sides.
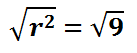 This gives us the radius.
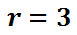 Now that we have the radius, we can draw the circle. The blue-colored ring is the actual circle. It is the set of points and the points are all three units from its center.
 Take a look at our quizmaster and activity. They will test your knowledge of equations of a circle to determine if you have digested this information on circles. Use the links that follow.
| |
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
|
Here are activities related to the lessons above.
|
Here related lessons to view.
|
 uiz:
uiz:  ctivity:
ctivity:  esson:
esson: