Flight of a Projectile | ||
| ||
Introduction | ||
In this section, you will learn how to model the flight of a projectile using a polynomial function. Here are the sections within this lesson:
|
A projectile is an object that is given some energy to cause it to go up, reach a maximum height, and then fall to the ground. The projectile can be a soccer ball, rock, bullet, baseball, or cannon ball. These objects all take on the same characteristic arc as they fly through the air. Soccer balls get kicked, rocks and baseballs get tossed, and bullets and cannon balls all fly through the air with a characteristic upside-down u-shape.

We will not examine spin, friction, or aerodynamics. We will simply look at three parameters explained within the next section.
| |||||||
The flight of a projectile depends on three variables in order to model its flight through space: the gravity on Earth, the starting height of the projectile, and the amount of vertical force given to launch the projectile.
To put all this information together, we are going to use a polynomial. [See our lesson, Operations of Polynomials, for further study.] Polynomials have variables, exponents on the variables and numbers in front of the variables, called coefficients. Here is our general polynomial function.
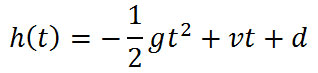
The polynomial function depends on the variable 't,' which stands for time. When we plug in values for time, the formula provides us with corresponding height values. If we plot these corresponding values as ordered pairs, we will get a graph that shows us the height of the projectile over time, which is different than the actual path of the projectile.
| |||||||
There are several methods for finding the maximum height of a projectile and the time it gets there. In this section you will learn how to find that height and time using algebra. Use the following video.
If you are interested in learning of the origins of the algebra formula for finding the time value when the projectile reaches its maximum height (the x-value of the vertex of a parabola), watch the video marked with the 'v,' immediately below. Caution: It is suggested that you first watch the two prerequisite lessons so that you will understand the video. If you already know how to complete the square and understand translations (transformations), then skip the lessons and go straight to the video.
In the following two sections, a graphing calculator will be used to locate the maximum height of projectiles and the time at which they return to the ground.
| |||||||
Let's look at an example problem and see how we use it to make a specific function.
If a projectile has an initial height of 50 feet and it's given an initial upward velocity of 100 feet/second, write a formula that describes the height of the projectile over time and determine all of its critical points. The first step is to identify the values in the problem. The 50 is the initial vertical distance (height) of the projectile, 'd.' The 100 is the initial vertical velocity, 'v.' Since we are on Earth, the gravitational force is 32. So, our specific polynomial function is this.
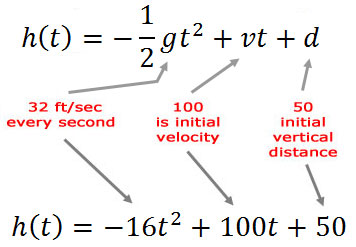
Notice that half of 32 is 16. The next steps involve graphing the polynomial function. Graphing it can be easily accomplished with the use of a graphing calculator. There are several great graphing calculators available from Casio and Texas Instruments. There are also several online graphing calculators that can graph. Here is what the graph of our specific polynomial function looks like.
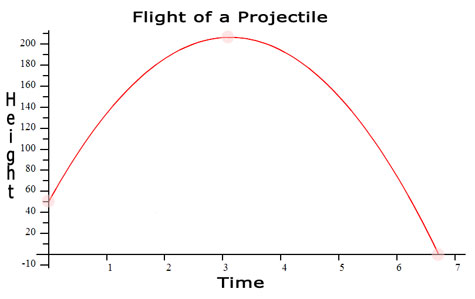
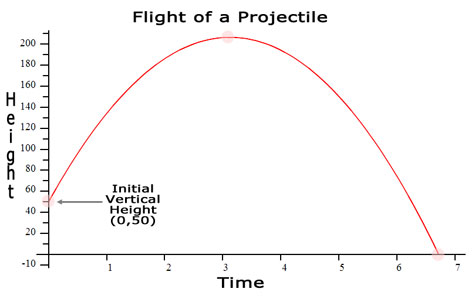
Keep in mind that the horizontal dimension (→) represents time and the vertical dimension (↑) represents the vertical height of the projectile. So, think of each point on the graph as (time, vertical height), not (x,y), and the rest of this lesson will be much more clear. There are three important locations on the graph. Those points can be easily located using various features of a graphing calculator, like adjusting its "window," using "zoom::fit," "trace," and other commands. Each graphing calculator is a little different. Here is the first important point on the graph, which is the initial height of the projectile.
The second point is the maximum height of the projectile.
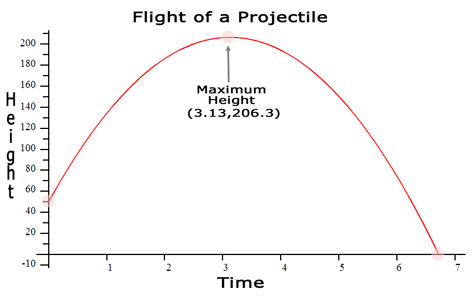
The last important point is the location on the graph that describes when the projectile reaches the ground.
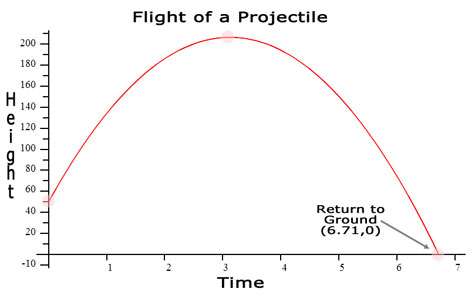
Let's examine those points a little bit more closely.
(0,50): Initial Height
The first value is time and the second is height. So, at t=0 seconds the projectile is at h=50 feet.
(3.13,206.3): Maximum Height
At t=3.13 seconds the projectile is at h=206.3 feet.
(6.71,0): Return to Ground
At t=6.71 seconds the projectile is at h=0 feet or ground level.
Now we know all the critical times and heights of this projectile. It reaches its maximum height of 206.3 feet at 3.13 seconds. It reaches the ground after a total of 6.71 passes from the time the projectile was launched. Now, test your own skills with a problem of your own. Use the interactive quiz to try a problem.
| |||||||
It is time to take a look at another problem. Here is how it may be written.
Locate the maximum height, time it reaches the maximum height, and the time at which the following projectile lands to the ground. The projectile has an initial height of 100 feet and it has an initial upward velocity of 400 feet/second. Let's identify the parameters of this projectile. The velocity is 400 ft/sec, so v=400. The initial height is 100 feet, so h=100. We can also assume it is on Earth, so g=32 ft/sec every second. We can now put those values into the general polynomial function.
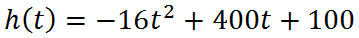
Using a graphing calculator, we determine the shape of the graph. This is what the graph of the specific polynomial function looks like.
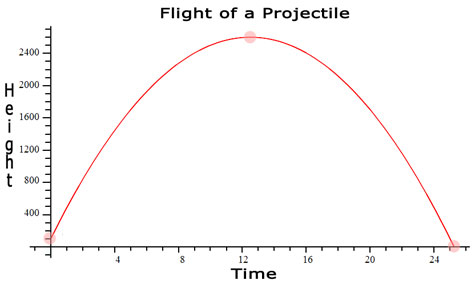
The graph below has all of the critical points located.
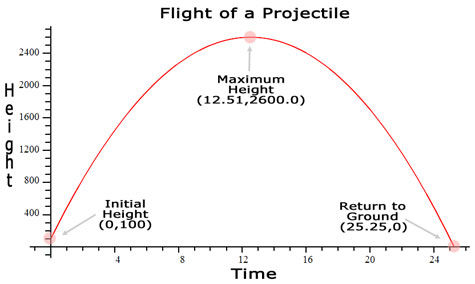
Here are the critical points analyzed to more depth.
(0,100): Initial Height
The first value is time and the second is height. So, at t=0 seconds the projectile is at h=100 feet.
(12.51,2600.0): Maximum Height
At t=12.51 seconds the projectile is at h=2600.0 feet.
(25.25,0): Return to Ground
At t=25.25 seconds the projectile is at h=0 feet or ground level.
Now we know all the critical times and heights of this projectile. It reaches its maximum height of 2600.0 feet at 12.51 seconds. It reaches the ground after a total of 25.25 seconds passes from the time the projectile was launched. Now, test your own skills with a problem of your own. Use the interactive quiz to try a problem.
| |||||||
There is a common misconception when dealing with the flight of a projectile. When given a function that defines height in terms of time, h(t), the graph of h(t) is not the actual path of the projectile. It is a picture of the height of the projectile in comparison to time. The graph below does nothing to tell us about the horizontal position of a projectile.

In order to see the actual path of the projectile, we would have to know the horizontal and vertical values of the projectile (and possibly the depth if we are dealing with space). The video below will demonstrate how to use parametric equations to plot the actual path of a projectile. This video will show how each point that describes the path will be represented with three values, namely time, height, and horizontal distance.
| |||||||
Try our instructioal videos to learn more about the lessons above.
| |||||||
Try our interactive quizzes to determine if you understand the lessons above. | |||||||
Try this activity related to the lessons above.
| |||||||
Try this lesson, which is closely related to the lesson above.
| |||||||
 esson:
esson:  ideo:
ideo:  uiz:
uiz:  ctivitiy:
ctivitiy: