Multiplying Fractions | ||
| ||
Introduction | ||
This lesson will inform you how to multiply fractions. Here are the sections within this lesson page:
|
To multiply fractions it is important to know how to reduce fractions. It is strongly recommended that you review this lesson before progressing with the following sections.
| |
There are many problems that require the multiplication of fractions. There are routine problems (determining how much paint to buy for a project) all the way up to applications problems (calculating how to mix chemicals to obtain a desired specific mixture). Here are two types of lessons in mathematics that require the multiplication of fractions.
The following section will help you understand how to multiply fractions.
| |
Like all skills within the realm of mathematics, there is a process to follow. For instance, determine what half of eight is. Intuitively, we know half of eight is four. This is what the mathematics looks like.
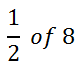
First, the word “of” refers to multiplication (most of the time).
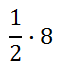
Change the 8 to a fraction, 8 divided by 1.
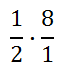
Now, multiply straight across. Multiply numerator times numerator. Multiply denominator times denominator.
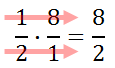
We know that 8/2 means 8 divided by 2. So, we continue.
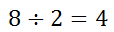
Of course, this is a long way to go to take half of 8. However, it lets us know how to do more difficult problems. As an alternative method, we could have reduced fractions before we multiplied across the two fractions. Look at this point in the problem.
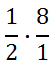
We could have found a common factor between 8 and 2, which is 2. In other words, we can divide both the 8 and the 2 by 2, like so.
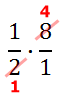
Now we can multiply across.
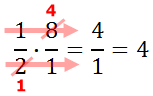
Reducing the problem makes it easier because the numbers are smaller, making the multiplication easier to perform.
The following sections will reveal more difficult problems.
| |
Here is our first example.
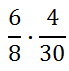
There are several ways to start reducing these fractions. Nevertheless, we can divide the 8 and the 4 by 4.
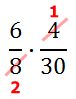
Now, we can divide the 6 and the 30 by 6, like so.
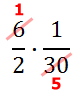
Since there is nothing left to reduce, we can multiply across.
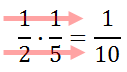
| |
Here is our second exmaple.
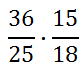
Before multiplying these fractions, first reduce a numerator with a denominator. We can divide the 15 and 25 by 5, like so.
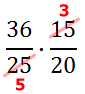
Next, we can divide the 36 and the 20 by 4, like so.

Since there is nothing left to reduce with a numerator and a denominator, multiply across, as seen below.
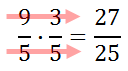
| |
Use this instructional video to learn how to multiply fractions.
| |
Use this interactive quiz determine if you know how to multiply fractions. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: