In this lesson, you will learn how to work with sigma notation. Here are the sections in this lesson.

• Series of Numbers
• Elements of Sigma Notation
• Related Lessons

    When we add lists of numbers, each of those lists of numbers is called a series.

    For instance, if a frog moves 12 inches in the first minute, 15 inches in the next minute, and 18 inches in the third minute and follows this pattern for 20 minutes, we may want to know how much distance the frog travels for those 20 minutes. The series would look like this.

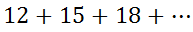
    This series does not continue on forever. It ends at its 20th number.

    You may recognize this to be an arithmetic series (see Arithmetic Sequences and Series) because the common difference is equal to 3.

    We could find the 20th term, once we gain a formula for the nth term. The formula for the nth term is...

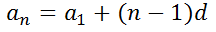
...where a₁ is the first term and 'd' stands for the common difference. So our general term is...

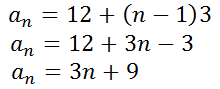
    Now we can find the last term, the 20th term of this series.

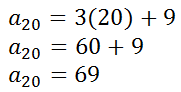
    Now we know that our series looks more like this.

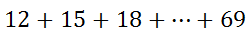
    In our next section, we will see how this series can be expressed in sigma notation.

    Sigma Notation looks like this.

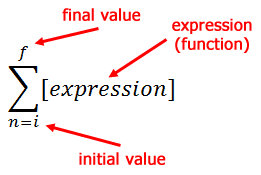
    The i-value is the initial value or starting value. The f-value is the final value or ending value. The expression refers to a mathematical expression, which we call a function (see Functions). The giant-sized "E" is the Greek symbol sigma.

    For the frog series that we were working on in our last section (see Series of Numbers), we can write the series using sigma notation, like so.

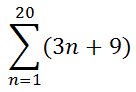
    If we were to plug in the starting value, n = 1, into the expression and evaluate it, we would get 12. Twelve is the first term of our series. Likewise, if we were to plug in n = 2 into the expression, evaluating it would yield 15. Plugging in n = 20 into the function yields 69.

    The sigma means we must find the sum of all those values, or...

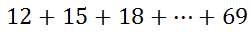
    Luckily, there is a formula that we can use to find this sum, which is this formula.

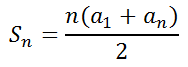
    Plugging in the relevant values gives us this.

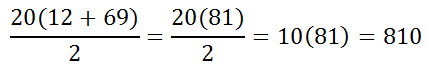
    Therefore...

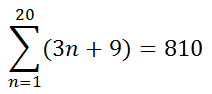
    Try these lessons, which are related to the sections above.

    esson: Functions
    esson: Arithmetic Sequences and Series
    esson: Sigma Notation: Arithmetic Series
    esson: Sigma Notation: Geometric Series