Parametric Equations | ||
| ||
Introduction | ||
This lesson page will inform you about parametric equations. Here are the sections within this lesson page:
|
Parametric equations are equations that define the location of points using another variable. Usually, the independent variable is represented as a t-value while the x and y-values are written as functions of ‘t.’ Here is an example of parametric equations that define a set of points in a plane.
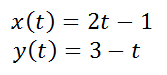
Notice that the equations have been written in function notation. Recall, this means x(t) is a function called 'x' that is being defined using a t-variable.
In the next section, you will be shown how to use these equations to get the corresponding graph.
| |
To gain a graph from parametric equations, choose values for the t-values and then evaluate the x and y-values. Here is a table that can be used for this purpose.
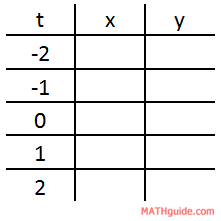
To calculate the x-values, plug in the t-values in the function one at a time. Here is one such calculation.
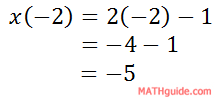
Likewise, we can do the calculation for the corresponding y-value.
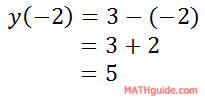
So, here is the first row in the table filled in.
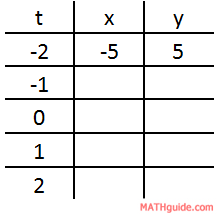
If we continue this process for all the t-values, we get these results.

If we wanted to graph this data, we need only look at the second two columns, which are the columns that reflect the x and the y-values.
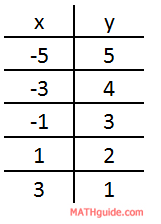
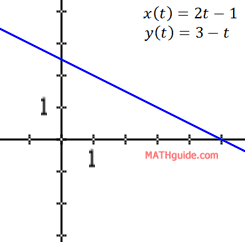
The graph of these points form a line.
| |
If given a set of parametric equations, it may be necessary to collapse them to a single equation without the parameter. The algorithm for doing this is easily explained. Here is that strategy.

Let us examine two examples, one simple and the other not so simple, to see how this algorithm is used. Example 1: Convert these parametric equations to a single equation.
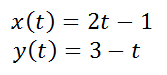
We should start with the second equation because it is easier to solve that equation for 't,' like so.
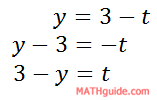
Now, we can use this equation to substitute for the t-value in the first equation.
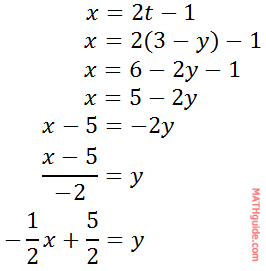
The next example will be a little bit more difficult. Example 2: Convert these parametric equations to a single equation.
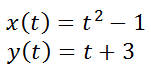
First, we need to solve one of the parametric equations for 't.' Picking the second equation would be the easier of the two equations.
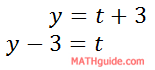
Now, we can substitute this expression for 't' into the first equation.
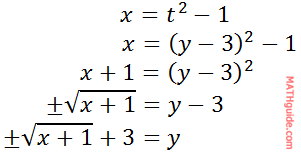
One could leave the equation like so...
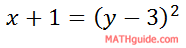
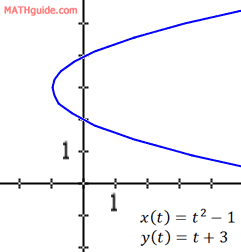
...as long as we understand that this is a sideways parabola (opens to the right).
| |
This instructional video will help you understand how to graph parametric equations. | |
Use these activities to learn about parametric equations.
| |
Use this interactive quiz to test your skills.
| |
Review these related lessons.
| |
 ideo:
ideo:  ctivity:
ctivity:  uiz:
uiz:  esson:
esson: