Graphing Logarithmic Functions | ||
| ||
Introduction | ||
This lesson will inform you how to graph logarithmic functions. Here are the sections within this lesson page:
|
In order to graph logarithmic functions, first learn what an exponential function looks like. This is important because the two functions are inversely related. This means knowing how exponential functions behave is a prerequisite for understanding logarithmic functions. Before proceeding with the following sections, it is strongly recommended that you first review these lessons.
| |
If we graph an exponential function and its corresponding logarithmic function, we will see an interesting geometric relationship. Below, an exponential function and its inverse have been graphed.
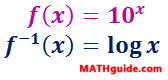
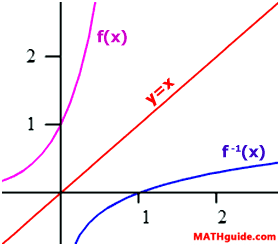
The graph of f(x), which is an exponential function, has the asymptote y = 0 and an y-intercept equal to (0,1). Inversely, the graph of f-1(x), which is a logarithmic function, has the asymptote x = 0 and an x-intercept of (1,0).
Knowing what inverses mean and the fact that exponential functions and logarithmic functions are inverses makes it easy to remember the shape and properties of logarithmic functions.
| |
The properties of transformations of functions are the same regardless of the function. This graphic organizer details those properties.

The sections below will details how these properties visually apply to logarithmic functions.
| |
Here is a logarithmic function.
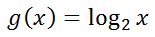
If we wanted to move g(x) 1 unit to the right, all we need to do is replace the x-value with (x–1), like so.
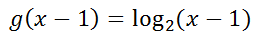
Placing both of these functions on the same coordinate system will reveal this shifting property.
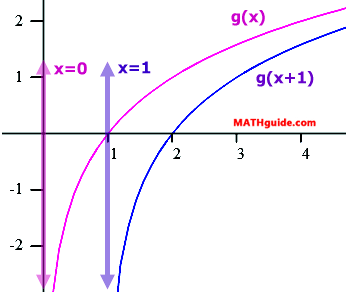
Also note that the asymptote and the x-intercept of g(x), which is x = 0 and (1,0) (respectively), is moved 1 unit to the right for the shifted curve. This means the vertical asymptote of the shifted curve is x = 1 and the x-intercept is (2,0). Likewise, if we wanted to shift g(x) 3 units to the left, all we need to do is replace the x-value in g(x) with x + 3, like so.
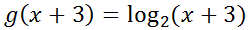
Use a graphing calculator to see that the curve is indeed shifted 3 units left and that its asymptote and x-intercept is shifted along with it, making the asymptote equal to x = -3 and the x-intercept (-2,0).
| |
Again, we will start with the function g(x).
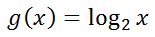
If we would like to move this curve vertically upward, all we need to do is add numbers to g(x). For instance, let’s add 1 to g(x) to see it move up 1 unit.
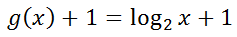
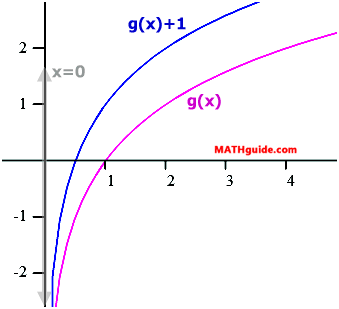
The graph of the transformed function has moved one unit up. Notice that the vertical asymptote, x = 0, has not been affected. This is because moving a vertical line vertically has no affect. Finding the x-intercept can easily be done with a graphing calculator: (see ‘trace’ feature). To find the x-intercept by hand, use a y-value of 0 because all points on the x-axis have a y-value equal to zero. Here is the mathematics.
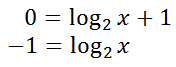
Changing from logarithmic form to standard form (see our lesson Converting Between Logarithmic and Exponential Forms), we get…
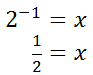
So, the x-intercept is (0.5,0), which is verified by looking at the graph of this translated function. The same transformation occurs when a function like g(x) has a number subtracted from it. If we subtract 1 from g(x), we get this function.

Graphical inspection of this transformation will verify that it is the result of moving g(x) 1 unit down, which is left to you to verify with a graphing calculator.
| |
If the opposite of a function is compared to the function, an interesting visual effect can be seen. Look at g(x) and its opposite function.

Both of these functions are shown below.
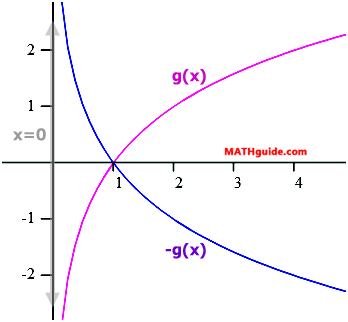
The function g(x) and its opposite exist as mirror images of each other if a mirror is imagined to be resting on the x-axis. It is said the x-axis is a line of symmetry for g(x) along with its opposite function –g(x). Notice that the x-intercept (1,0) and the asymptote (x = 0) were not affected by the reflection.
| |
Review these two examples in order to fully grasp transformations on logarithmic equations. Example 1: h(x)=log3 (x-2) - 1 If we were to graph h(x), we would need to rely on its parent function, which is…
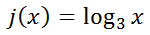
This curve has the typical shape of a logarithmic curve; it has a x-intercept of (1,0) and the vertical asymptote x = 0, as shown by this graph.
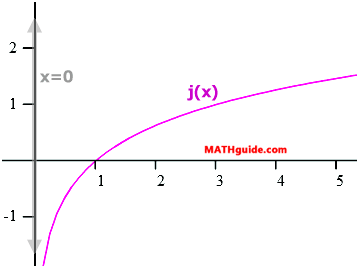
To graph h(x), we need to move j(x) 2 units right and 1 units down. Here is j(x) shown with h(x).
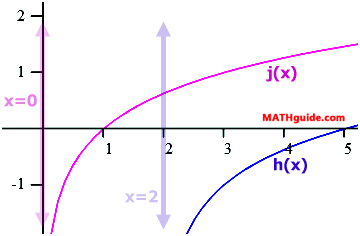
Because the curve has been moved 2 units right, the new asymptote is no longer x = 0, but instead x = 2. However, the x-intercept is harder to determine with exact certainty. We will use a y-value of 0 to find the x-intercept as follows.
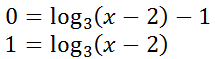
Changing the logarithmic equation to exponential form, we get this equation and continued solution.
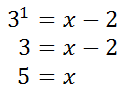
Therefore, the x-intercept is equal to (5,0). This is verified by viewing the graph above. Example 2: k(x)=-2log3 (x+1) + 5 To graph this function, we must perform four tasks. Here are those tasks.
To determine the x-intercept, we will again use a y-value of 0 and solve for ‘x,’ as follows.
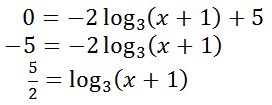
Changing the logarithmic equation to exponential form, we get this equation.
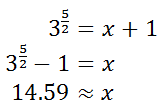
So, the x-intercept is close to (14.6,0). Use a graphing calculator to verify this x-intercept.
| |
This video will help you understand the transformation sections above. | |
This quizmaster will help you assess your understanding of the lessons above. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: