Inverse Functions | ||
| ||
Introduction | ||
In this section, you will learn about inverse functions. Here are the sections within this lesson:
|
MATHguide has a lesson on functions. Functions tell us how to use mathematical expressions with values substituted for variables to arrive at important quantities. We may want to calculate the area of a room to order carpet. We may want to determine the volume of a cylindrical tank to know how much water it can hold or the the amount of money earned in interest for a bank account. If we were investigating the scene of an accident, we may want to calculate the speed of a car based upon the length of the skidmark it left on a road. Inverses of functions are needed when we want to work backwards and solve functions and relations for the independent variable(s).
First of all, the idea of inverses is one that should be familiar to us. In grammar school we learned there are operations on numbers that are inverses. We learned multiplication and division are inverse operations. Before that, we learned addition and subtraction are inverse operations. We will use inverse operations to alter a function to gain its inverse function or inverse relation.
| |
The process for gaining an inverse functions requires two general steps. Here are those steps for functions that involve the variables x and y.
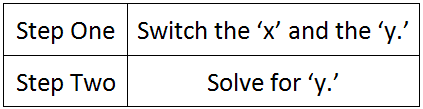
We will use these steps for a variety of problems below. However, we should take a quick look at the notation for inverses.
| |
When we seek to find inverse functions, there is notation to consider. If we start with this function
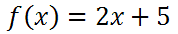
we first see that there is a peculiar f(x). If spoken, it is reads as f of x. It simply means y. So, we could instead write the problem like this.
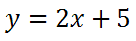
The directions for determining the inverse of a function can be written either of two ways:
Both of these directions are asking for the same result, namely the inverse of the original function, as we will see in the next section.
| |
This section, we will examine how to calculate inverses. Let s take a look at three examples. Example 1: Calculate the inverse of
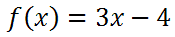
First, we will replace the f(x) with y, like so.
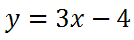
Step number one says we must switch the x and the y.
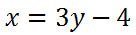
Step number two says we must solve for y. To do so, we will add 4 to both sides and get this new equation.
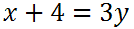
Next, we must divide both sides by 3.
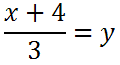
If we divide all the terms by 3, we get this.
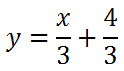
Alternately, we can write the solution like any of these representations:
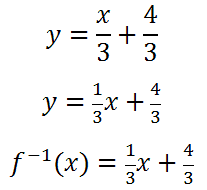
Each of them is mathematically equivalent to each other.
Example 2: Calculate the inverse of
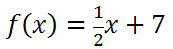
First, we will replace the f(x) with y, like so.
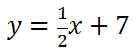
Step number one says we must switch the x and the y.
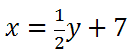
Step number two says we must solve for y. To do so, we will subtract 7 to both sides and get this new equation.
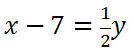
Next, we must multiply both sides by 2 to cancel the half.
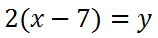
Doing the distributive property, we get this
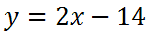
Alternately, we can write the solution using either of these representations:
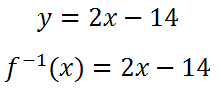
They are mathematically equivalent to each other.
Example 3: Calculate C -1 of
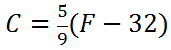
Let it be known, this is the formula that converts Fahrenheit temperatures into Celsius temperatures. As for the business of solving for its inverse, first we will replace the C with y and the F with x.
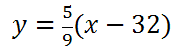
Step number one says we must switch the x and the y.
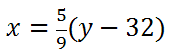
Step number two says we must solve for y. To do so, we will both sides by 9/5 to get this new equation.
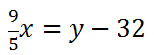
Next, we must add 32 to both sides to get this equation.
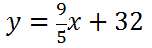
Since we found C -1, it means this is really the function that converts Celsius temperatures into Fahrenheit temperatures. Using letters, it means this
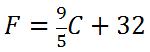
Our formula is backwards in a sense. Instead of using Fahrenheit temperatures to gain Celsius temperatures, the new formula does the inverse. It uses Celsius temperatures to gain Fahrenheit temperatures. This is the meaning of inverse as it applies to these temperature scales. Now, try a quiz to determine if you have mastered the lessons above.
| |
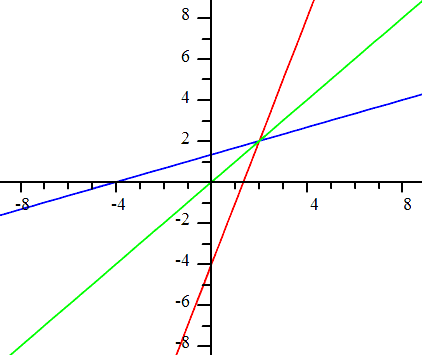
When graphing a function and its inverse function, there is a special visual property. The two curves will be symmetrical across the diagonal line, y = x. To demonstrate this visual relationship, we will look at three examples. Example 1:
Below is a graph that contains both of the given lines. The red line is the first line and the light green line is the diagonal line, y = x.
Example 2:
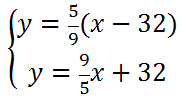
Below is a graph that contains both of the given lines. The red line is the first line and the light green line is the diagonal line, y = x.
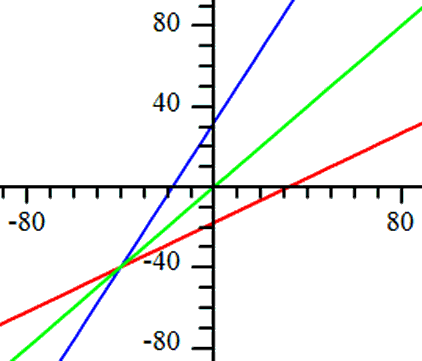
Example 3:
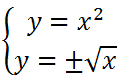
Below is a graph that contains both of the curves. This example contains non-linear relations. The red curve is the first relation and the light green line is the diagonal line, y = x.
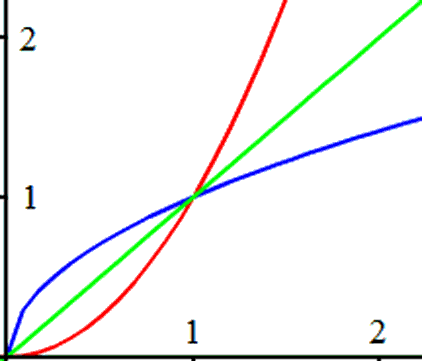
| |
Try our interactive quiz to determine if you understand the lessons above. | |
Try this activity related to the lessons above.
| |
Try this lesson, which is closely related to the lesson above.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: