Parallel versus Perpendicular | ||
| ||
Introduction | ||
This lesson page will teach you how to tell the difference when two lines (or segments) are either parallel or perpendicular. Here are the sections within this lesson page:
|
Here are the definitions of parallel and perpendicular.
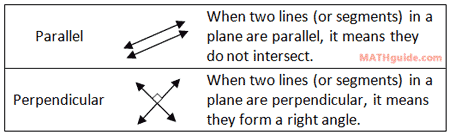
| |
When two lines (or two sides of a polygon) are parallel, their slopes will be equal. When two lines (or two diagonals of a polygon) are perpendicular, their slopes will be opposite reciprocals of each other. The table below encapsulates this information.
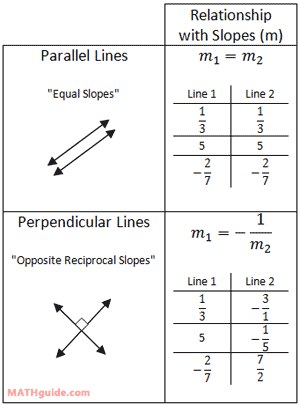
| |
These examples will show you how to determine when two lines (or segments) in a plane are either parallel, perpendicular, or neither of the two. The calculations for slope (see our Slope Formula lesson) have not been shown. Only the interpretations of the slopes are explained. Example 1: Given A(3,1), B(5,4), U(-5,10), and V(-3,13), what is the relationship between line-AB and line-UV? Are they parallel, perpendicular, or neither?
The slope between point-A and point-B is 3/2. The slope between point-U and point-V is 3/2. Since the slopes are equal, AB and UV are parallel lines.
The slope of line-RS is -1/2. The slope of line-KL is 2/3. Since these slopes are neither equal nor opposite reciprocal, these lines are neither parallel nor perpendicular.
The slope of line-CD is -2/1 or simply -2. The slope of line-GH is 1/2. Since these slopes are opposite reciprocal of each other, these lines are perpendicular. | |
This instructional video will help you understand hwo to determine when two lines (segments) are parallel, perpenducular, or neither.
| |
Try this interactive quizmaster to see if you understand this concept. | |
Try theses lessons, which are related to the sections above.
| |
 esson:
esson:  uiz:
uiz:  ideo:
ideo: