Classifying Parallelograms | ||
| ||
Introduction | ||
This lesson page will inform you how to classify parallelograms. Here are the sections within this lesson page:
|
This lesson that follows requires that you already know how to use the slope and distance formulas. If you are not familiar with these formulas or you would like to hone your skills with them, use the links below where you will find interactive quizzes and instructional videos.
It is also necessary to know how to use the slope formula to determine if lines (or segments of polygons) are parallel, perpendicular, or neither. Use this lesson to master this skill. | |
Most people know what parallelograms look like. Just in case, here is a look at them and their diagonals.
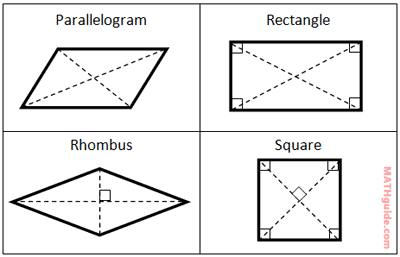
They are all parallelograms, but the rectangle, rhombus, and square have the properties of a parallelogram and more. Here is a list of their properties and their definitions.




These properties will enable us to be able to tell them apart, which is discussed in the following sections.
| |
When presented with the four vertices of a quadrilateral, it is possible to determine what type of parallelogram it is, or if it is not a parallelogram. All we need to do is familiarize ourselves with the slopes of both its diagonals and the slopes of its sides. This table shows us that by looking at those slopes, we can determine the best name for the quadrilateral.
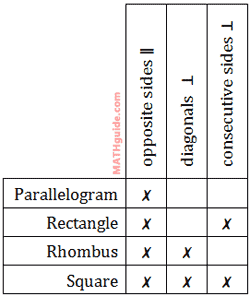
Looking horizontally across the table we can learn about parallelograms. A square has opposite sides that are parallel, consecutive sides that are perpendicular, and diagonals that are perpendicular. A rhombus has opposite sides that are parallel and diagonals that are perpendicular. A rectangle has opposite sides that are parallel and consecutive sides that are perpendicular.
A parallelogram has opposite sides that are parallel. If a quadrilateral is not a parallelogram, its opposite sides will not be parallel.
| |
The best way to learn how to use slopes to classify parallelograms is to review a problem. Here are two problems. Example 1: Given quadrilateral A(11, 5), B(3, 4), C(-1, -3), D(7, -2), classify it as the correct type of parallelogram. Here are the slopes of its sides:
The only parallelogram that does not have internal angles that are right angles but has perpendicular diagonals is a rhombus.
Here are the slopes of its sides.
 uiz: Classifying Parallelograms Using Slope uiz: Classifying Parallelograms Using Slope
| |
In the last section, we saw how we could use six slopes to classify a parallelogram. However, there is a method that involves four calculations, instead of six. If we focus solely on the diagonals, we can use their slopes and there distances to classify them. This table examines properties of diagonals to make our job slightly easier.
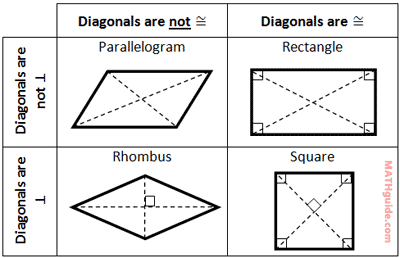
Here are two examples. Example 1: Given quadrilateral A(-7, 4), B(-12, 5), C(-6, 12), D(-1, 11), classify it using the slopes and lengths of its diagonals. Slopes of Diagonals
Example 2: Given quadrilateral A(-1, 0), B(7, -18), C(16, -14), D(8, 4), classify it using the slopes and lengths of its diagonals. Slopes of Diagonals
 uiz: Classifying Parallelograms Using Slope and Distance uiz: Classifying Parallelograms Using Slope and Distance
| |
Try these interactive quizmasters to determine if you understand how to classify paralleograms.
| |
Try these related lessons.
| |
 esson:
esson: