Solving Logarithmic Equations | ||
| ||
Introduction | ||
In this section, you will learn how to solve logarithmic equations. Here are the sections within this lesson:
|
This lesson requires you to know about a variety of properties of logarithms. Our previous lesson on logarithms explains how to:
If you are not already familiar with these skills, please study them before continuing with this lesson. | |
Here are two examples that demonstrate how to solve logarithmic equations that have logarithms on both sides of the equation. Example 1
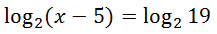
When two sides of an equation have the same logarithm (and the same bases on those logarithms), the inside expressions (called the arguments) must also be equal to each other. Consequently, we can make this equation.

Solving this rudimentary equation gives us the final solution, which is x = 24.
Example 2
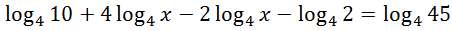
Notice both sides of the equation contain logarithms. However, the left side of the equation has several logarithms. When one side of a logarithmic equation has several logarithm terms, condense the logarithms down to a single logarithm. Remember, this only works when the logs have the same base. First, we need to move the coefficients of our logs and change them into exponents.
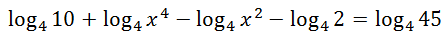
Second, the negative logarithms require us to place their arguments in the denominator of our new logarithm expression.
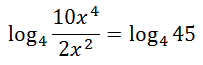
Third, we can simplify the argument of the left log expression.
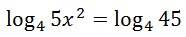
Fourth, notice how both sides of the equation have a single log of the same base. This means the inside expressions must be equal to each other. So, we can solve this equation.
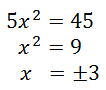
It appears that we have two solutions. However, if we were to test the negative value of -3 into the original equation, we would eventually have to take the log of a negative value. Since we cannot take the log of a negative value, -3 is called an extraneous solution. It must be discarded. So, x = 3 is the sole solution to this logarithmic equation. Watch this video that demonstrates how to solve logarithmic equations. | |
This section will help you to understand how to solve logarithmic equations that have a log on a single side of the equation. This also applies to situations when equations can be manipulated so that a logarithm will be found on a single side of the equation. Example 1

First, condense the left side. Remember, this only works when the logs have the same base. Let us start by moving the coefficients to exponents.
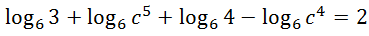
Also, negative logs require us to place their arguments into the denominator of our single log expression.
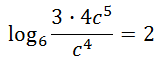
Let’s clean up that argument.
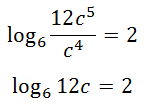
Next, since there is only a log on one side, we can rewrite the equation in exponential form.
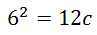
Last, solve the resulting equation.
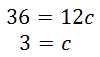
Example 2
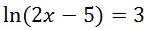
This problem certainly has a logarithm on a single side of the equation. Like one of the steps in our last example, we need to transform this logarithmic equation into an exponential equation. What is the base of this ln? Natural logarithms have a base of ‘e.’ (This ‘e’ is a transcendental number, like pi, but it is approximately equal to 2.718…) This equation can now be understood to be…
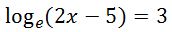
This logarithmic equation can be transformed into an exponential equation.
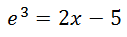
Finally, this equation can be solved, like so.
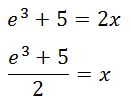
Watch this video that demonstrates how to solve logarithmic equations. | |
Watch this video that demonstrates how to solve logarithmic equations. | |
These lessons are related to the lesson above.
| |
 esson:
esson:  ideo:
ideo: