Surface Area of Common Solids | ||
| ||
Introduction | ||
In this section, you will learn how to calculate the surface area of common solids to include:
|
Within our area section, we had to provide a definition for the meaning of area. That definition rested upon the square -- particularly a unit square. A unit Square can be 1" x 1" or 1 yd x 1 yd or 1 ft x 1 ft or a square by some other unit.
We saw the area of a figure was nothing more than the sum of all unit squares of a figure. For the surface area of a solid, there is a similar definition, but it applies to the exterior surfaces of the solid. The definition of surface area is the sum of all unit squares that fit on the exterior of a solid.
| |||||||||||||||||||||||
SA = 2(lw + hl + hw) | |||||||||||||||||||||||
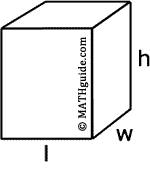
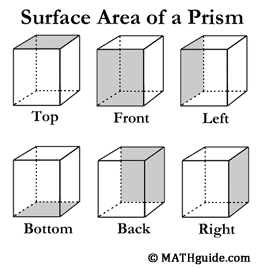
This is the best figure to begin with when investigating surface area. It is the most simple figure of all the solids. It is also a figure most people have personal experience due to either wrapping or opening gifts. All the surfaces of a prism are rectangular. This makes calculating the areas of these surfaces very easy to do. The area of rectangles have been discussed in another section, which is available for review before proceeding, if necessary. As the diagram below indicates, there are six surfaces to a rectangular prism. There is a front, back, top, bottom, left, and right to every rectangular prism. The surface are of a prism is nothing more than the sum of all the areas of these rectangles.
Using the labeling of the general prism diagram above, a formula can be created for dealing with the surface area of prisms. Let's calculate the area of each surface.
Example 1: Given l = 4 yds, w = 2 yds, and h = 5 yds, the surface area would be... SA = 2(lw + hl + hw)
Example 2: Given l = 6 mm, w = 9 mm, and h = 8 mm, the surface area would be... SA = 2(lw + hl + hw)
| |||||||||||||||||||||||
SA = 2πr2 + 2πrh | |||||||||||||||||||||||
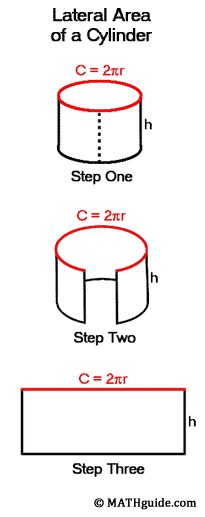
A cylinder has a total of three surfaces: a top, bottom, and middle. The top and bottom, which are circles, are easy to visualize. The area of a circle is πr2. So, the area of two circles would be πr2 + πr2 = 2πr2. The third surface, the lateral surface area, is less easy to visualize for the purposes of calculating its area, especially since it does not appear to be in a shape that fits a known area like a triangle or parallelogram. The surface being referred to is the curved wall of the cylinder.
Now, from the newly cut edge, the cylinder wall will be spread open. Almost like opening double doors to a fancy home, the walls spread apart. See step two of the same diagram. When the cylinder's wall is completely open, it takes the form a very recognizable, basic shape. It is a rectangle. Fortunately, the area of a rectangle is easy to calculate. But we need to go back to the original cylinder for a moment before we calculate the rectangle's area. The top of the original cylinder is a circle. We know that the distance around a circle is called its circumference, C = 2πr. The circumference has been marked in red. When the cylinder wall is completely open, we see that the circumference of the circle becomes the length of the final rectangle. The dimensions of the rectangle are the circumference, C = 2πr, and the height of the cylinder, h. So, the area of the rectangle is A = l x w = C x h = 2πr x h = 2πrh. Finally, if we put all the three surfaces together, we can arrive at the formula for the complete surface area of a cylinder. The top, the bottom, and the walls of the cylinder (the lateral surface area) determine the total surface area. Those values are πr2 + πr2 + 2πrh = 2πr2 + 2πrh. Sometimes this expression is written as 2πr(r + h) in certain geometry texts. [Can you see how 2πr2 + 2πrh is equal to 2πr(r + h) by the distributive property?]
Example 1: If r = 6 ft and h = 4 ft, then the surface area would be... SA = 2πr2 + 2πrh
Example 2: If r = 5 cm and h = 2 cm, then the surface area would be... SA = 2πr2 + 2πrh
| |||||||||||||||||||||||
SA = s2 + 2sl | |||||||||||||||||||||||
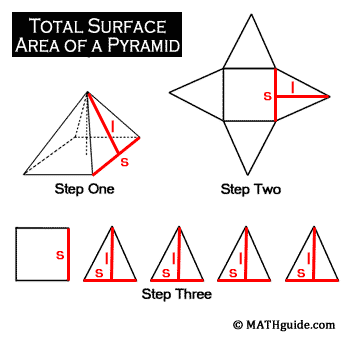
Pyramids that have a square base have a total of five surfaces. To determine the shapes of those surfaces, we will start with a pyramid from step one below. If we cut along the lateral edges of the pyramid, we can allow the figure to flatten out in step two below. From step two, the individual figures are easily identified as a square and four triangles.
We can use the area formulas for a rectangle and a triangle to determine the complete formula for the surface area of the pyramid. The square (or base of the solid) has an area that can be calculated by multiplying its length times its width. Since those dimensions are equal, the area is s x s = s2. Now we need to calculate the area of the remaining surfaces. The remaining surfaces happen to form the lateral surface area of the pyramid, which are triangles. The area formula for a triangle is its base times its height divided by two. In the case of one of the triangles above it would be s x l ÷ 2. However, there are four triangles. This would make the total lateral surface area equal to four times the area of one triangle, or 4 x s x l ÷ 2. Upon simplifying the expression, we get 2sl. The total surface area of the pyramid is equal to the area of the base plus its lateral surface area or s2 + 2sl. So, given the base length of the pyramid, s, and its slant height, l, the total surface area is not a difficult computation. Yet, when dimensions are provided for a pyramid, one is rarely provided with the slant height, l. Instead, the height of the pyramid is given. This is an important difference, as one is always larger than the other.
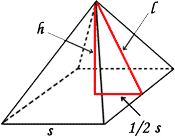
A right triangle, which rests internally within the pyramid, has been highlighted. The hypotenuse (longest side) is the slant height of the pyramid, l. This is the length we need to know in order to calculate the surface area of the pyramid. The height of the pyramid is a leg of the right triangle. The base of the right triangle is half the length of the base edge of the pyramid, s. At this point, we would use The Pythagorean Theorem to calculate the slant height. Pythagoras said leg2 + leg2 = hypotenuse2. In the case of our right triangle, we would get (1/2 s)2 + h2 = l2. Solving for the slant height would then depend on our ability to use the Pythagorean Theorem. To review the process, there is an outline of the steps that need to be taken:
Here are two examples that demonstrate how to calculate the total surface area of a pyramid.
Example 1: Given: s = 8 m and h = 3 m. First we calculate the slant height using The Pythagorean Theorem and half the base length. Example 2: Given: s = 7 in and h = 6 in.
First we calculate the slant height using The Pythagorean Theorem and half the base length.
| |||||||||||||||||||||||
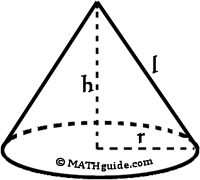
SA = πr2 + πrl | |||||||||||||||||||||||
Example 1: Given r = 4 m and h = 3 m.
First we must calculate the slant height using The Pythagorean Theorem. Example 2: Given r = 7 in and h = 10 in.
First we must calculate the slant height using The Pythagorean Theorem
| |||||||||||||||||||||||
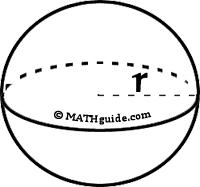
SA = 4πr2 | |||||||||||||||||||||||
Example 1: Given r = 3 ft.
The surface area requires the use of the formula... Example 2: Given diameter = 20 m or r = 10 m.
The surface area requires the use of the formula...
| |||||||||||||||||||||||
Use these videos to solidify your understanding of these solids.
|
After reading the lessons, try our quizmasters. MATHguide has developed numerous testing and checking programs to solidify these skills:
|
Here are activities related to the lessons above.
|
Here are related lessons.
|

 ideo:
ideo:  uizmaster:
uizmaster: 
 ctivity:
ctivity: 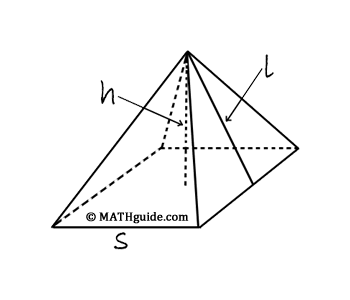
 esson:
esson: