Polar Coordinates | ||
| ||
Introduction | ||
This lesson page will inform you about polar coordinates. Here are the sections within this lesson page:
|
When graphing a point in the Cartesian coordinate system, we do so using horizontal and vertical movements. This is similar to moving through a city that has nothing but East-West and North-South streets. There is another system for graphing points in a plane, called the polar system. This system has its points defined by their distance from the origin and their angle from the positive x-axis.
The following section will explain how to graph polar points.
| |
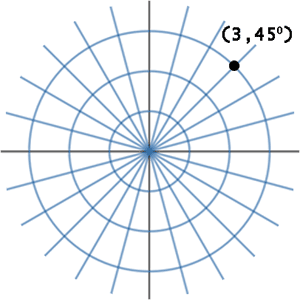
Here are two examples of graphing polar coordinates. Example 1: Graph (3, 45°). To graph this point, imagine starting at the origin and looking down the positive x-axis. It is as if you are standing at the origin and looking east. Next, rotate 45° counter-clockwise and then move 3 units from the origin.
Example 2: Graph (2, 210°). Starting at the origin while facing east, turn 210° counter-clockwise. Then, move 2 units from the origin. This is what the result looks like.
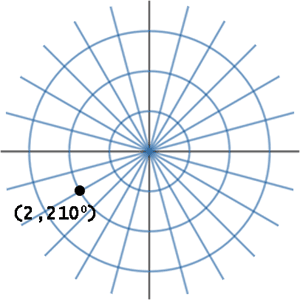
| |
To convert from rectangular to polar coordinates, we have to use two equations. Here are those equations.
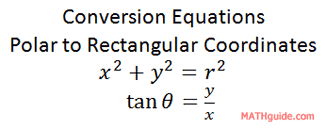
The equations relate to the definition of the cosine and sine functions.
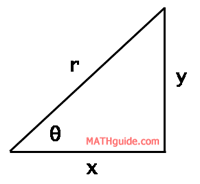
Cosine is defined as adjacent (x) over hypotenuse (r). Likewise, sine is defined as opposite (y) over hypotenuse (r). With a little algebra, we can solve for ‘x’ and for ‘y’ to achieve the conversion equations shown above. Here are two examples. Example 1: Convert (2,135°) to rectangular coordinates. For a purely algebraic solution, we can solve for the x-value and the y-value as follows, keeping in mind that r=2 and θ= 135°.
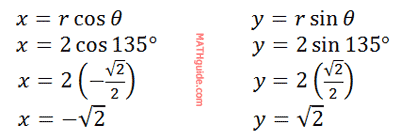
So, the point in rectangular form is…
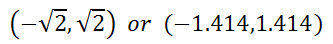
Example 2: Convert (-1,330°) to rectangular coordinates. Solve for the x-value and the y-value using the equations. Remember, r=-1 and θ= 330°.
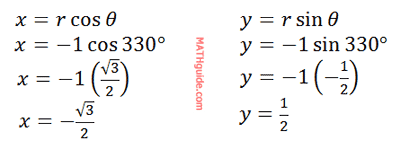
So, the point in rectangular form is…
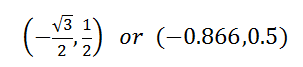
| |
To convert from rectangular to polar coordinates requires different equations. Here are those equations.
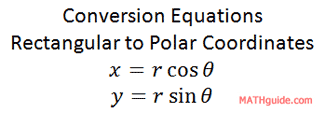
To understand the genesis of these equations, examine this diagram.

The relationship between the x, y, and r-variables should be familiar. Since this is a right triangle, we can employ The Pythagorean Theorem, which is the first of the two conversion equations. Using knowledge of trigonometry, we can see the tangent of theta is equal to the opposite (y) over adjacent (x) sides, which is the second conversion equation. Now, let us look at two examples to see how these conversions are done. Example 1: Convert (5,-3) to polar form, rounded to the nearest tenth. It is helpful to get a diagram to see what is going on. Here is the graph of the rectangular point.
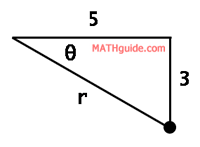
To get the distance the point is from the origin, which is the r-value, we will use the first conversion equation, like so.
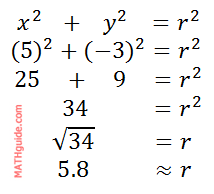
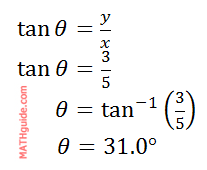
Remember, this angle is the reference angle. Since the angle exists in the fourth quadrant, we have to account for the traditional trigonometric angle relative to the positive x-axis with a counter-clockwise motion. Therefore, the angle is 360° - 31° = 329.0°. So, the final answer, written as (r, θ), is…
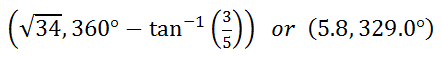
Example 2: Convert (-1, √3) from rectangular form to polar form. Here is a diagram of the point in the second quadrant.
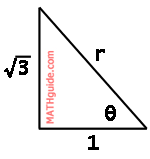
It is unnecessary to calculate the length of the hypotenuse if you recognize this special right triangle. Assuming you do not recognize the triangle, let us view the calculation using the first conversion equation.
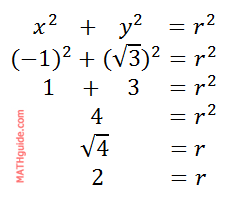
Now, we must calculate the angle using the second conversion equation (if you do not recognize the special right triangle). Since we already know the angle exists in the second quadrant, only positive values are being used.
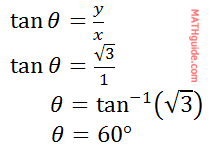
Remember, this is the reference angle not the angle to the positive x-axis. The angle to the positive x-axis (rotating in the typical counter-clockwise fashion) is 120°. Last, we need to write the point in (r, θ) form as…
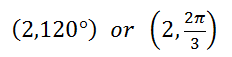
| |
This instructional video will help you understand polar coordinates. | |
These interactive quizzes will help you understand polar and rectangular coordinates.
| |
Review these related lessons.
| |
 ideo:
ideo:  uiz:
uiz:  esson:
esson: