In this lesson, you will learn how to determine the period and the equation of a musical note. Here are the sections within this lesson:

• Sounds are Waves
• Example 1: Calculating B-Value, Writing Equation of Sine Function
• Example 2: Calculating B-Value, Writing Equation of Sine Function
• Instructional Videos
• Interactive Quizzes
• Related Lessons

    Every sound is a wave of particles. Whether the sound is traveling through air, a metal train track, or water, particles contract and expand in waves.

    There are many different kinds of sounds. There is noise, like a radio that isn't tuned in to a channel, and there is purposeful sounds, like the sounds made when a blacksmith hammers iron into various shapes.

    There is also music. Music is a collection of notes that are usually placed into interesting patterns: progressions, rythmic beats, juxtaposed tones, ...

    Let us examine a single note. Various notes have specific wavelengths. For instance, the note A₂, has a wavelength approximately equal to 320 cm. A graph of A₂ would look like this.

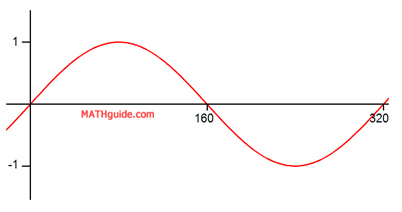
    The horizontal axis is in centimeters. The vertical axis is less important because relates to volume. Whether the note is soft or loud is unimportant because it is the note that is the thrust of this lesson.

    If we wanted to determine the equation of this note, we will use a sine function. We will use the sine function because the wave of the graph that is shown passes through the origin. [We could as easily use a cosine function for this purpose as it would also demonstrate an equation of the same musical note.]

    Recall that the period of a sinusoid has this formula (see our lesson Graphing Sine, Cosine, and Tangent: Calculations for more details).

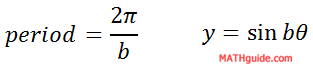
    To determine the b-value of the equation, we must replace the period in the equation with 320 and then solve this equation.

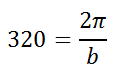
    To solve it, cross-multiply.

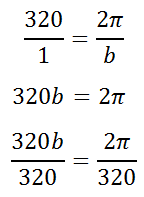
    Now, we can reduce the fraction on the right side.

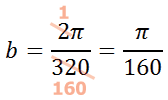
    So, we can replace the b-value in the equation with ^π/₁₆₀, like so.

      ideo: Sound Waves to Sine Waves
      uiz: Equation of a Musical Note

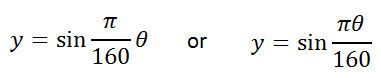
    The note D₂ has a wavelength approximately equal to 470 cm. Imagine if we were asked to sketch a graph and determine its equation.

    Its graph can be expressed as a sine wave with a wavelength of 470, like so.

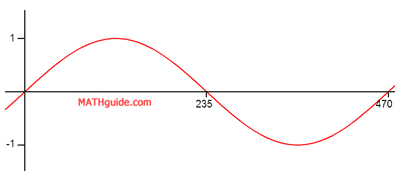
    We can calculate the b-value of the equation by using the formula for period. Replacing the period with 470, this is the work we need to do.

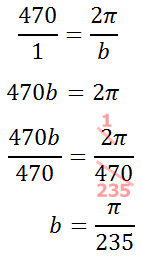
    Therefore, the equation for a D₂ note is...

      ideo: Sound Waves to Sine Waves
      uiz: Equation of a Musical Note

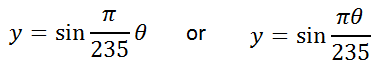
    Watch this instructional video that will allow you to understand how to get the equation of a sine function to match a musical note.

      ideo: Sound Waves to Sine Waves

    Here is an interative quiz that will help you to determine if you understand this lesson.

      uiz: Equation of a Musical Note

    Try this advanced lesson, which is closely related to the lesson above.

      esson: Graphing Sine, Cosine, and Tangent