Geometry Proofs | ||
| ||
Introduction | ||
In this section, you will learn how to graph conic sections. Here is a list of the sections within this webpage:
|
Logic is a huge component of mathematics. Students are usually baptized into the world of logic when they take a course in geometry. However, there is plenty of logic being learned when studying algebra, the pre-cursor course to geometry.
However, geometry lends itself nicely to learning logic because it is so visual by its nature. This is why the exercise of doing proofs is done in geometry. This lesson page will demonstrate how to learn the art and the science of doing proofs.
| |
All proofs are separated into two columns. There are statements on the left-side and reasons on the right-side. See the diagram below to see how they look.
 All proofs start with given information. That given information is placed into the left-side, under 'statements.' The reason would be 'given information.' From that starting statement/reason, the rest of the proof is done.
Every statement that gets entered into the proof needs to be justified by either information that is given or information that logically flows from predetermined facts.
| |
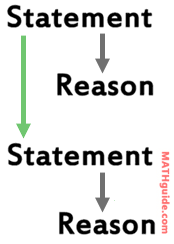
You will be provided with a video in this section. It will demonstrate how to do simple proofs. Pay close attention to how every statement must be justified with a reason. Notice how each reason is placed to the right of every statement so that a person reading the proof can follow along in the mind of the person doing the proof, as seen in the graphic below.
 Watch this video to see how the logic of basic proofs is done. Here is a table of statements and follow up statements to help you do your own proofs.
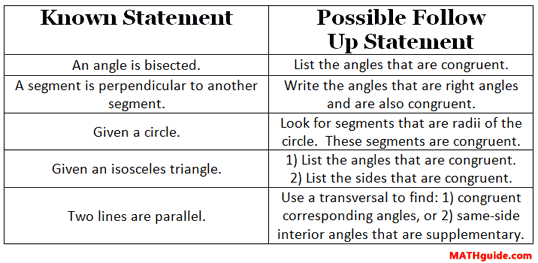
This table can help us use statements to arrive at statements that logically follow. We will need this type of thinking to be successful at Moderate Level Proofs.
| |
In our last section, we saw how Beginner Level Proofs work. This section will show us how statements logically link together with other statements to form flows of thought. While it may not necessarily be the case, a great way to prepare for harder levels of problems is by proving triangles are congruent, using one of the five methods, listed in this table.
Many problems geometry students face deal with triangle congruence. Be aware that some people have trouble with proofs because they fail to see how statements can be used to form new statements, as demonstrated by this diagram.
 Let this video show you how to prove two triangles are congruent based upon different given situations. | |
Advanced level problems usually incorporate triangles that are congruent, but then go beyond that. To go beyond congruent triangles, we have to use something called CPCTC. It means this.

When two triangles are congruent to each other, it is like a super bonanza. All respective elements are congruent. It means there are three pairs of congruent angles and three pairs of congruent sides. Often, proving triangles congruent leads to being able to prove a variety of other grandiose conditions.
|
Here are videos related to the lessons above.
|
Now that you have looked at several facts related to proofs, it is time to put your skills to the test. The interactive quiz in this section will present you with problems. They start out simple, but they get progressively more difficult. Use the drop-down menus to enter your answers. Happy proof-ing!
|
Here are related lessons to view.
|
 ideo:
ideo:  uiz:
uiz:  esson:
esson:  esson:
esson: