Adding and Subtracting Fractions | ||
| ||
Introduction | ||
This lesson will inform you how to add and subtract fractions. Here are the sections within this lesson page:
|
To understand the sections below, it is necessary to know how to reduce fractions. It is strongly recommended that you first review how to reduce fractions before proceeding.
| |
Reducing Fractions requires dividing the numerator and the denominator of a fraction by a common factor. Scaling up fractions is the reverse. First, let us look at a fundamental rule of mathematics. Consider this fraction.
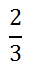
We could multiply this fraction by the number 1. Doing so would not change its value.
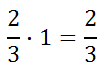
Since 4/4 is also equal to 1, we can multiply 2/3 by 4/4 and not change its value.
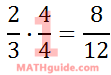
Reducing 8/12 by dividing the top and bottom of the fraction by 4, we getů
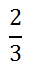
So, we can scale fractions up however we please. Look at these fractions, each being multiplied by 1 to scale them up.
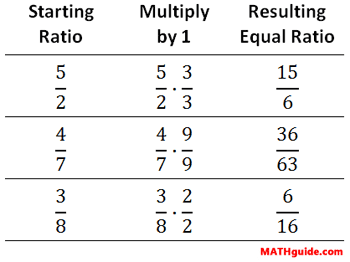
It can be seen that scaling up fractions is the opposite of Reducing Fractions.
This skill will be used in the following sections.
| |
Look at this example.
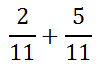
Both fractions are referring to 11ths. Therefore, the numerators can be added while keeping the same denominators, like this.
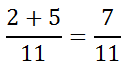
Since the fraction cannot be reduced (the numerator and denominator have no common factor, other than 1), 7/11 is the final answer. The fractions with this next example can be combined with little effort.
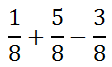
The reason why this can be handled with little effort is because all the fractions have the same denominator. They are all in 8ths. To combine them, keep the same denominator and combine all of the numerators, like so.
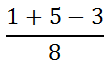
Cleaning this up, we getů
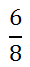
This fraction can be reduced.
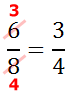
So, 3/4 is the final solution.
The next sections will explain how to add/subtract fractions that have unlike denominators.
| |
Assume you were asked to add these fractions.
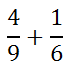
Notice that the fractions have unlike denominators. We cannot add them until the denominators are equal. First, we will have to decide what the common denominator can be. To get this common denominator, consider the multiples of the denominators, which are 9 and 6.
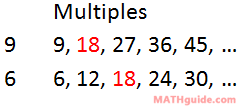
By looking at the table above, we can see that 9 and 6 have a common multiple. It is 18, which has been colored red. Next, we need to scale up the factors so that the new denominators have this common multiple. To help the process, the problem can be arranged vertically, like so.
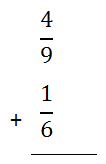
We must change the denominators to that of their common multiple, which is 18. With that in mind, new fractions next to the existing fractions will be made but so that the new denominators are 18.
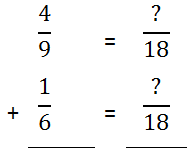
Since the 9 in the denominator must be multiplied by 2 to get 18, the 4 must also be multiplied by 2.
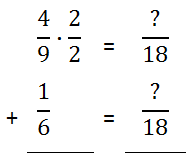
Likewise, the 6 in the other denominator must be multiplied by 3 to get 18; so, the numerator must be multiplied by 3, too.
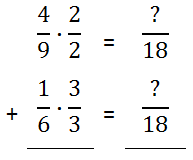
The new fractions can be obtained by multiplying across, as the next graphic will indicate.
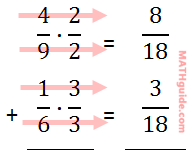
Now that the denominators are equal, we can add the fractions on the right to get this answer.

Since 11 and 18 share no common factor (other than 1), it cannot be reduced, which makes it the final answer.
| |
The last section explains how to add fractions with a considerable amount of detail. This section will provide slightly less detail. Here is a subtraction problem.
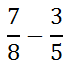
First, we must search for a common multiple using the denominators, 8, and 5.

Now that we have the common denominator of 40, we can set up our problem vertically. 40 has been placed in the fractions to the right.
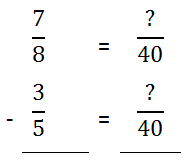
We need to multiply the first denominator by 5 and the second denominator by 8 and then multiply across.
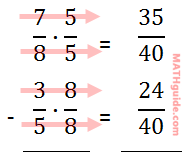
Since the denominators are now equal, we can subtract the numerators.

11 and 40 have no common factors (other than 1), which makes 11/40 the final solution.
| |
Use this instructional video to understand how to add and subtract fractions. | |
Use this interactive quiz to determine if you can add and subtract fractions. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  ideo:
ideo:  uiz:
uiz: