Limits of Ratios of Polynomials | ||
| ||
Introduction | ||
This lesson page will how to calculate the limit of ratios of polynomial functions. Here are the sections within this lesson page:
|
This page will explain how to evaluate limits of ratios of polynomial functions. They will be of either of these forms.
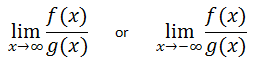
By looking at each of those limits, it is clear we are taking a look at trends that are occurring far from the origin -- the extreme right and extreme left.
| |
When we consider polynomial functions within limits, we need to know what it is that determines the value of the function for extremely small and extremely large values. Take this function, f(x).
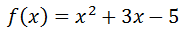
It has three terms: x2, 3x, and -5. For large x-values, the -5 hardly does anything to the value of the function. All one has to do is evaluate the function at x = 100 to see which term dominates the result.
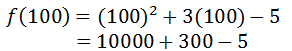
Adding the last two terms results in 295, which is very close in value to 300, not -5. Also, adding 295 and 10000 gives us 10295, which is very close to 10000. 10000 was the result of the squared term. The squared term dominates the value of the result. Here is one more value to consider, f(1000).
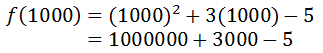
Again, the value obtained from the squared term, 1 million, is much greater in value than either of the two values. We can try substituting extremely small values, like x = -1000, but the same affect will be found. [Try it for yourself.]
This means the values gained from the term with the greatest exponent dominates all the values obtained from the terms with the smaller exponents.
| |
Sometimes we are faced with limits of ratios of functions. Given two polynomials f(x) and g(x), we need to evaluate...
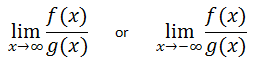
...here is a handy graphic that summarizes three cases.

The following sections will explain why it is these three results occur.
| |
Here is an example of a ratio of polynomials such that the degree of the numerator is less than the degree of the denominator.
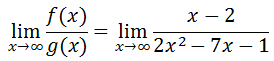
If we examine a table of values of increasing x-values, a clear pattern can be seen.
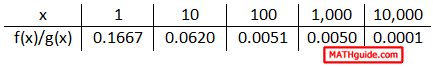
It is evident that the ratio's value is approaching zero as the x-values increase. Here is a table that examines what happens when the x-values get smaller.
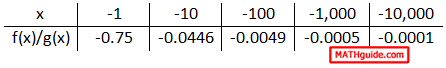
This ratio also approaches zero when the x-values get smaller. The reason why this happens relates to the degrees of the polynomials. When g(x) has a greater degree than f(x), g(x) produces values that are far greater than those generated by f(x). Taking a number and dividing it by a much greater number produces a small result. The result gets smaller and smaller as the x-values increase. For the same reason, the result gets smaller and smaller as the x-values decrease. This pattern always occurs when the denominator has a greater degree than the numerator. Written using mathematical symbols, it can be written like so. Given polynomials f(x) and g(x), if deg(f(x)) < deg(g(x)), then...
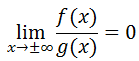
| |
Here is a ratio of polynomials such that the degree of the numerator is equal to the degree of the denominator.
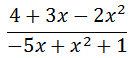
It is not immediately apparent that the degree of the numerator and denominator are equal until we write the polynomials in descending order, like so.
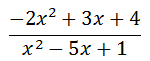
Now it is clear that both of the polynomials are degree two. If we look at the ratio of polynomials on an analytical level, we can determine its value as the x-values either increase or decrease. For instance, we know that the terms of a polynomial that have the highest degree dominate the value of the polynomial for very large (and very small) x-values. This can allow us to look for long-term trends by examining the leading coefficients of the two polynomials.
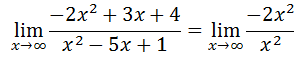
Furthermore, we can reduce the ratio of polynomials.
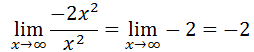
This shows us that the ratio of polynomials will approach the value -2 as the x-values increase. This limit is also the same as the x-values decrease; so, the work will not shown. If we examine a table of increasing x-values, it will verify our conclusion.
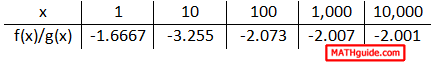
It is clear that the value of the ratio of polynomials is heading toward -2 as the x-values are increasing. Likewise, this next table of values will show us a trend as the x-values decrease.
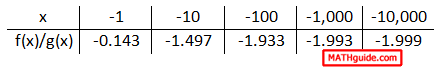
The trend for decreasing x-values is clear. The value of the ratio of polynomials is heading toward -2 and our conclusion is sound. Yet, this is an explanation that holds for a single example. We need to look at this from a wider scope. In general terms, this is what a ratio of polynomials looks like.
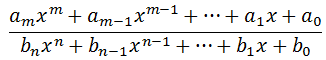
Keep in mind we are maintaining that the numerator and denominator have equal degrees, which means the m-value is equal to the n-value. If we look at these polynomials with respect to extremely large x-values (or very small x-values), we need only examine their leading coefficients to grasp the trend they would have.
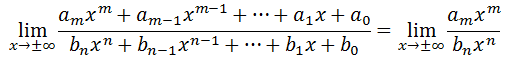
Since m = n (their degrees are equal), we can further simplify the limit to be...
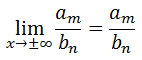
The long-term trend is simply the ratio of the leading coefficients of the original polynomials. | |
Let us examine a ratio of polynomials such that the degree of the numerator is greater than the degree of the denominator.
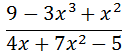
Again, we know when we are considering large x-values that the value of the polynomial is most influenced by the term that contains the highest degree. So, if we consider the limit of our ratio for large x-values, we get...
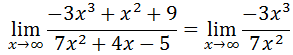
We can simplify the new ratio, like so.
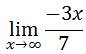
Upon inspection of the simplified ratio function, we can see it is linear. If we were to graph the function, we would see that it flows down to the right. This means that the value of the function will continuously decrease as the x-values increase.
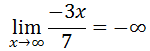
Likewise, if we perform the same calculation for small, decreasing x-values, we will get the same simplified ratio. [The work is not shown.]
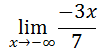
However, now we are looking at the extreme left-side of the graph of this ratio function. If we examine the graph of the ratio function, the left-side of the linear function continuously goes up as the x-values decrease. This makes our limit...
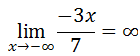
If we were to examine several cases when the degree of our polynomial in the numerator is larger than the degree of the polynomial in the denominator, we would see something interesting.

Regardless of the ratio of polynomials we begin with, our simplified ratio results with another polynomial. We know that polynomials have end behavior that is based on their degrees and leading coefficients. [Review our lesson on End Behavior if you do not recall this property of polynomials.] This means our ratio of polynomials will either approach infinity or negative infinity, depending upon the coefficient and degree of the simplified ratio. Written mathematically, we get this: Given polynomials f(x) and g(x), if deg(f(x)) > deg(g(x)), then...
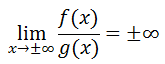
To determine if the limit is either positive or negative infinity, we will need to look carefully at the degree and leading coefficient of the polynomial. | |
Try these lessons, which are related to the sections above. | |
Try these lessons, which are related to the sections above.
| |
 esson:
esson:  uiz:
uiz: