Dot Product of Vectors | ||
| ||
Introduction | ||
This lesson page will explain what a vector dot product is. Here are the sections within this lesson page:
|
The dot product between vectors u and v is written like this.

This may look like multiplication, but within the realm of vectors it is called a 'dot product.' To calculate the dot product of two vectors we have to find the sum of the products of their respective components, like so. If u = <uh,uv> and v = <vh,vv>, then their dot product is calculated as:
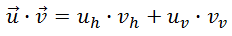
The result will be a scalar quantity. In other words, the result is a number. Example 1: Calculate a · b for a = <5,-2> and b = <-4,-1>. Here goes the calculation.
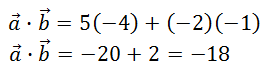
Example 2: Calculate c · d for c = <-8,4> and b = <-3,-10>. Let's calculate the dot product.
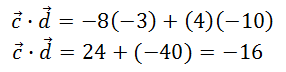
Try our quizmaster to determine if you have absorbed how to calculate the dot product of vectors.
| |
There are two methods for calculating the dot product of two vectors, you can see the first method with examples in the previous section, Dot Product Calculation. Here are both of the methods together. Method 1:
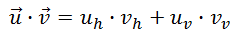
Method 2:
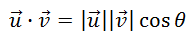
...where θ is the angle between the two vectors. We can test this by looking at an example. Let us look at the case u = <1,0> and v = <1,√3>. Here are the vectors graphed together.
Now, let us perform the calculations. Method 1:

Method 2:
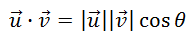
Vector u is a unit vector, so...
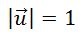
Although the Pythagorean Theorem is not shown for v...
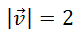
This is evident when we draw a vertical line to create a right triangle and place the lengths next to its sides. We can see these two vectors create a 30-60-90 triangle as shown here:
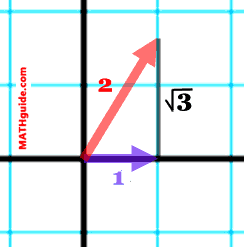
It can be seen the angle between the two vectors is 60°. Continuing with the method 2 calculation, we get the following.
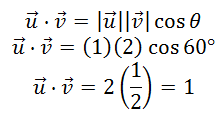
This is evidence that both methods for calculating the dot product are equivalent to each other. Method 2 provides us with the best opportunity for understanding what dot product mean on a graphical level. Simply put, it is a measure of how much two vectors have in common. This can be demonstrated by looking at two vectors in a plane.
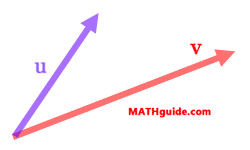
The image can be rotated so that v is horizontal.
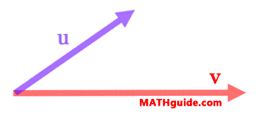
If we were to shine a light directly, far above v, u would cast a shadow on top of v, like so.
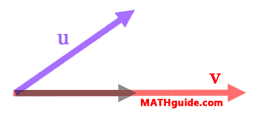
The length of the shadow vector can be found by doing a little bit of trigonometry -- seen below.
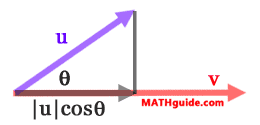
So, to calculate the dot product, we would then multiply these quantities because they are both aligned in exactly in the same direction.

We can rearrange the right side of the equation to yield this.
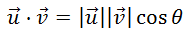
This is method 2, which was gained through a graphical understanding of what the dot product represents. It can be viewed as: 1) a measure of how much two vectors have in common, or 2) a measure of how much two forces are working together.
| |
When the dot product of two vectors is equal to zero, it has special meaning. It means the two vectors are orthogonal (perpendicular).
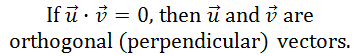
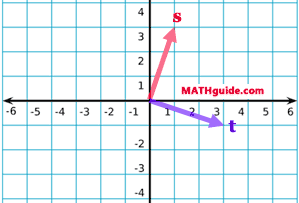
Recall this relationship: When two lines are perpendicular, then the slopes of the lines must be opposite reciprocal to each other. So if one line has a slope of 2/3, then the other line must have a slope of -3/2. A similar relationship is true for vectors. Imagine s = <1,3>. Let's take a look at it on the Cartesian plane.
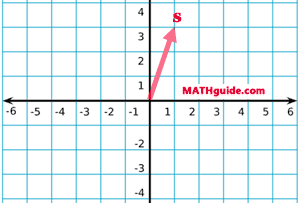
The slope (rise/run) of s = 3/1. If we took the opposite reciprocal of 3/1, we would get -1/3. We could create t that had the same slope, such as <3,-1>. We will now calculate the dot product of s and t.
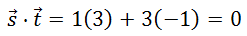
Let us take a look at s and t on the same Cartesian plane.

Clearly, both the graph of the vectors and the dot product show there is validity to the claim about orthogonal vectors having a dot product equal to zero, but it is not a proof. Here is a paragraph proof and justification via algebra:

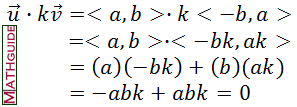
It is confirmed. Can you determine when two vectors are orthogonal? Use this quizmaster to find out.
| |
Try this video to learn more about the information above.
| |
Try these quizzes to see if you understand the content above.
| |
Try these lessons, which contain more information on vectors.
| |
 esson:
esson:  uiz:
uiz:  ideo:
ideo: