Graphing Sine, Cosine, and Tangent | ||
| ||
Introduction | ||
In this webpage, you will learn how to graph sine, cosine, and tangent functions. Here are the sections within this webpage:
|
The graphs of trigonometric functions have several properties to elicit. To be able to graph these functions by hand, we have to understand them. Before we progress, take a look at this video that describes some of the basics of sine and cosine curves.
| |
The video in the previous section described several parameters. This section will define them with precision within the following table.
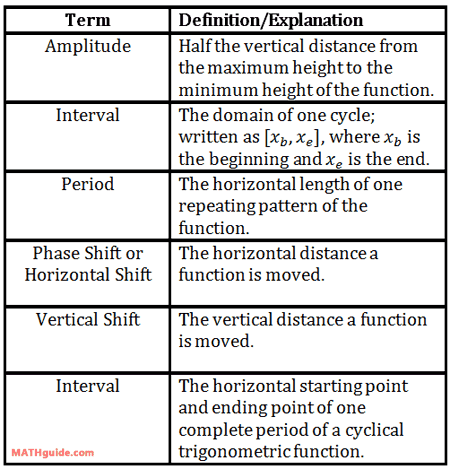
| |
Amplitude and Period | |
To calculate amplitude and period, the equation of our sine and cosine curves have to be in a specific form. The equations have to look like this.
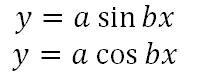
Once in that form, the parameters for amplitude and period are calculated as follows.
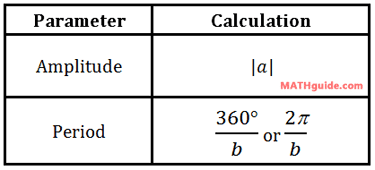
| |
Amplitude and Period | |
Here is a sine function we will graph.
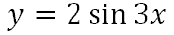
The a-value is the number in front of the sine function, which is 2. This makes the amplitude equal to |2| or simply 2. The graph of the function has a maximum y-value of 2 and a minimum y-value of -2. The b-value is the number next to the x-term, which is 3. This means the period is 360 degrees divided by 3 or 120. So, the curve has a y-intercept of zero (because it is a sine curve it passes through the origin) and it completes one cycle in 120 degrees. This is the graph of the sine curve.
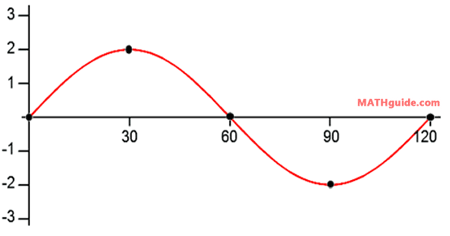
This particular interval of the curve is obtained by looking at the starting point (0,0) and the end point (120,0). The domain (the x-values) of this cycle go from 0 to 120. So, we write this interval as [0,120]. This video will demonstrate how to graph a different sine function with two parameters: amplitude and period.
| |
Amplitude and Period | |
Here is a cosine function we will graph.
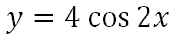
The a-value is the number in front of the sine function, which is 4. This makes the amplitude equal to |4| or 4. The graph of the function has a maximum y-value of 4 and a minimum y-value of -4. The b-value is the number next to the x-term, which is 2. This means the period is 360 degrees divided by 2 or 180. So, the curve has a y-intercept at its maximum (0,4) (because it is a cosine curve) and it completes one cycle in 180 degrees. This is the graph of the cosine curve.
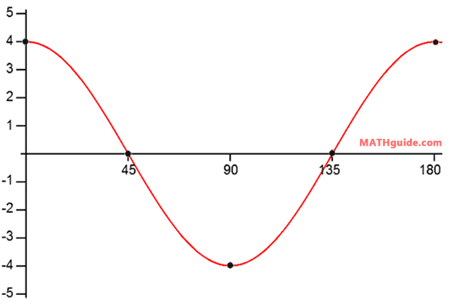
This particular interval of the curve is obtained by looking at the starting point (0,4) and the end point (180,4). The domain (the x-values) of this cycle go from 0 to 180. So, we write this interval as [0,180]. This video will demonstrate how to graph a different cosine function with two parameters: amplitude and period.
| |
Phase Shift and Vertical Shift | |
To calculate phase shift and vertical shift, the equation of our sine and cosine curves have to be in a specific form. The equations have to look like this.
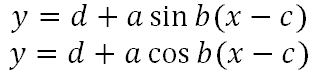
Once in that form, all the parameters can be calculated as follows.
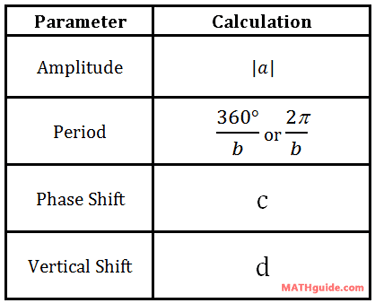
Notice that the equations have subtraction signs inside the parentheses. The c-values have subtraction signs in front of them. However, the phase shift is the opposite. This will be demonstrated in the next two sections.
| |
Amp, Period, Phase Shift, and Vert. Shift | |
This video will demonstrate how to graph a sine function with four parameters: amplitude, period, phase shift, and vertical shift.
| |
Amp, Period, Phase Shift, and Vert. Shift | |
This video will demonstrate how to graph a cosine function with four parameters: amplitude, period, phase shift, and vertical shift.
| |
Word Problem | |
The ocean level rises and falls. It is referred to as the tide. This video will explain how to use a set of facts that are laid out in a word problem and create the equation of a sinusoid. The equation will quantify the height of the tide over time.
| |
Period and Phase Shift | |
This video will demonstrate how to graph a tangent function with two parameters: period and phase shift.
| |
Try our instructional videos on the lessons above.
| |
Here is an interative quiz.
| |
Here are activities replated to the lessons in this section.
| |
Try this advanced lesson, which is closely related to the lessons above.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: