Placement Counting | ||
| ||
Introduction | ||
In this section, you will learn how to use the formulas for combinations and permutations for various placement problems. Here are the sections within this lesson:
|
What do bookshelves, scrambled letters, seating people at a restaurant, and town maps (grid problems) have in common? On the face of it, these things all seem like different problems. They certainly are different types of problems, but their solutions involve interesting similarities, as we will see below. | |
As we arrange books on a bookshelf, there are a few different types of counting problems. Let’s take a look at a few of them. Example 1:
“If there are three math books, five science books, and four English books, how many ways can they be arranged on a shelf if all the books are different books?” There are a total of twelve books to place on the shelf. Picture twelve places on our shelf, which will be represented using blanks below.
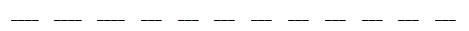
There are twelve possible books for our first space on the shelf.
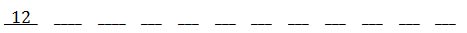
Once chosen, there are eleven books to use for the second space on the shelf.

Since two books have been shelved, there are ten books that can now be placed on the shelf.
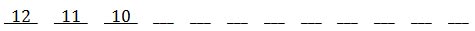
We will continue this pattern until all books are used, which gives us these numbers.
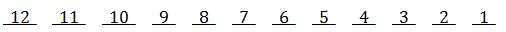
The Fundamental Counting Principle requires us to multiply these numbers. Multiplying them is the same as…
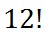
Example 2:
“If there are three math books, five science books, and four English books, how many ways can they be arranged on a shelf if all the books are different books and we arrange them by subject?” First, we have to realize that there are math books to place on the shelf. We can use blank spots to represent the books, like so.
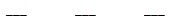
If we place one book on the shelf at a time, we can see there are 3 possible math books we could place on the shelf, first.
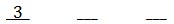
Once a book is on the shelf, there are 2 possible books to place next on the shelf.
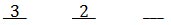
This leaves only 1 book to place last on the shelf.
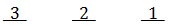
We multiply them, due to the Fundamental Counting Principle and get 3!. Likewise, when we place science books on the shelf, there are 5! Ways to do so. There are 4! ways to place the English books on the shelf. However, we have to consider how many ways we can now place these books, by subject. Since there are three subjects (math, English, and science), there are 3! ways to arrange them on the shelf. Here are those arrangements:

There are 3! ways or six ways to arrange the subjects. Putting this all together, we get this is our answer:
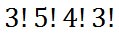
...which is 103,680 ways to arrange all the books by subject.
| |
There are interesting problems involving words. We could be given a word and be asked to determine how many ways we could scramble up the letters to get a new arrangement of letters. Here are a few problems. Example 1:
“How many ways can the letters from the word ‘champion’ be made to form a new arrangement of letters?” This is very similar to our book problem. Instead of books, we have letters to place. There are eight letters to rearrange. So, there are this many ways to arrange them:
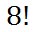
Example 2:
“How many ways can the letters from the word ‘beginning’ be made to form a new arrangement of letters?” First of all, there are nine letters to rearrange. So, there are this many ways to arrange those letters:
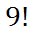
This problem is a little different, however, than example 1. The reason it is different is because there are letters that repeat. If we were to switch the placement of the two ‘g’s, we would not gain a new arrangement of letters. Rearranging the ‘g’s does not give us a distinguishably different arrangement. To account for these repeating letters, we have to see exactly which letters are repeating. We have two ‘g’s, two 'i's, and three ‘n’s. So, we are going to divide our initial answer by 2!, 2!, and 3!, like so.
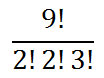
Example 3:
“How many ways can the letters from the word ‘toot’ be made to form a new arrangement of letters?” There are 4 letters. The ‘t’s repeat twice and the ‘o’s repeat twice. So, this is the answer.
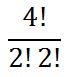
The numerical answer to our solution is this.
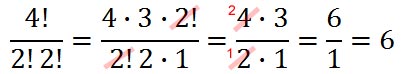
To verify this answer is indeed correct, here are the six ways to arrange the letters to gain distinguishably different arrangements of letters.
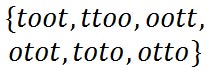
| |
There are two different types of problems involving seating people. Here are a few of those situations placed below as examples. Example 1:
“If there are four people who will be seated in a row, how many ways can it be done?” We will represent the seats with blanks, as we see below.
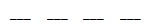
The first seat can be filled with 4 possible people. Once the first seat is filled, the second seat can be filled with 3 possible people, and so on.
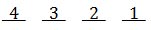
The Fundamental Counting Principle tells us to multiply the numbers, which would be…
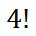
Example 2:
“If there are four people who will be seated at a circular table, how many ways can it be done?” This problem appears to be the same as example 1. Using letters to represent Anna, Bob, Conrad, and Dave, this would give us these possible arrangements if we used the same strategy.

However, some of these are the same, considering we are seating people at a circular table. For instance, arrangement “ABCD” is identical to “BCDA,” “CDAB,” and “DABC.” ‘Why are they alike?’ you may ask. In all cases, if we arrange people around the table in a clockwise fashion, Conrad has Bob to his right and Dave to his left, just like all the other members in relation to each other. Likewise, there are other arrangements that are identical, like “BCAD” and “CADB.” There are several others, too. Therefore, a circular arrangement of people of n-people is not simply n! arrangements of people in a circle. Instead, there are one fewer factorial number of people. If there are n-people to be seated at a circular table, there are (n-1)! unique possible arrangements. There is one less factorial because it really does not matter where the first person is placed at a circular table. Since we started with four people, this is our answer.
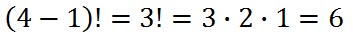
Going back to our list of solutions, these are all the unique placements.
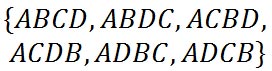
| |
In this section, we will examine a city grid – imagine East-West and North-South streets. We will be given a grid with people on opposite sides of it. We will have to determine the number of possible routes that can be traveled to go from one person to the other person. Example 1:
“Two people, Anna and Bob, are on opposite sides of a grid and we want to determine how many direct routes there are between them.”
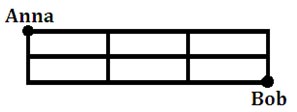
Bob has several choices for a path. One path he can take is:
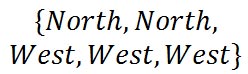
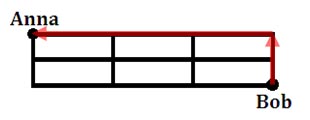
Let’s abbreviate that as {NNWWW}. We can scramble up these letters to find another possible path. Realizing this is asking us to count all possible arrangements of these letters, we can see this is exactly like our section, Scrambled Letters, above. There are a total of two ‘N’s and three ‘W’s. That is five letters to scramble. However, we have to adjust for the repeating letters and divide by the respective factorials, like so.
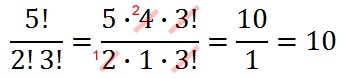
There are ten unique paths. Example 2:
“Jim wants to retrieve his dog, King, who are both located within the points marked on the map below. How many routes can Jim take to get to King?”
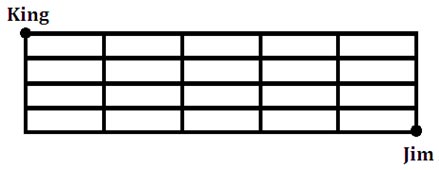
One possible path Jim could take is this:
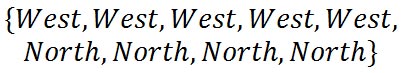
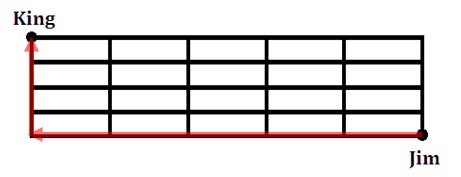
Let’s abbreviate that as {WWWWWNNN}. We can scramble up these letters to find all possible paths. To do so, we can see there are 9 path directions, but ‘W’s repeat 5 times and ‘N’s repeat 4 times. This gives us:

There are 126 unique paths.
| |
Try our instructional videos.
| |
Try our interactive quizzes to see if you understand.
| |
Try these activities related to the lessons above.
| |
Try these lessons, which are closely related to the lesson above.
| |
 ideo:
ideo:  uiz:
uiz:  ctivity:
ctivity:  esson:
esson: