Parabola in Vertex Form | ||
| ||
Introduction | ||
In this section, you will learn about parabolas in vertex form. Here is a list of the sections within this webpage:
| ||
A parabola is in vertex form if it looks like this.
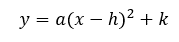
The a-value cannot be 0, else the function will not be a parabola. However, the h-value and k-value can be any values.
When the parabola is in this form, its vertex will be at (h,k). The examples below will make this clear.
| ||
Here is a specific equation of a parabola that is in vertex form.
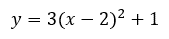
Here is its graph.
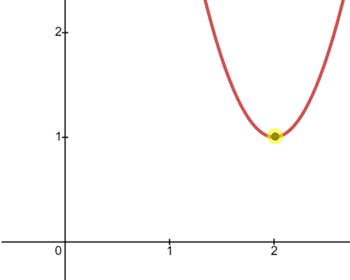
Notice that its minimum point, called the vertex, is located at (2,1). Also, the leading number, which is a positive 3, tells us the parabola must be concave up. This, too, is verified by looking at its graph because its branches go up. Here is another equation of a parabola in vertex form.
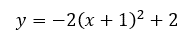
Here is the graph of the parabola.
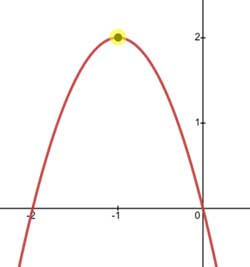
Look at the location of its maximum point, which is its vertex. It is located at (-1,2). The x-value of the vertex is the opposite of the factor.
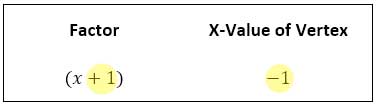
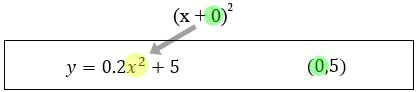
This is not a coincidence. When the parabola is written in vertex form, the x-value of the vertex will always be the opposite of its factor. The y-value of the vertex will always be equal to the trailing number at the end of the equation. Here are some examples.

The last equation has nothing in the parentheses with the x. So, the x-value of the vertex is zero.
| ||
The leading number in front of the equation informs us of the concavity of the parabola. Here are some examples.

The last parabola is concave up because the coefficient of the x2-term is positive. If there is no coefficient in algebra, we can imagine a one being there, like this: x2 = 1x2. To further make sure the previous characteristics are understood, here is a problem.
Problem The concavity of the parabola tells us what type of number to place as a leading number within the equation. Since the parabola is concave down, a negative number has to be the leading number. Any leading number will work. The vertex (2,5) tells us what to use for the other numbers. Since the x-value of the vertex is 2, the factor must be the opposite, (x - 2). The y-value of the vertex is 5; so, the trailing number of the equation must be 5. Putting it all together, we get...
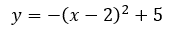
This is not the only possible answer. The leading number must be negative, but it does not have to be any special negative value. In fact, all the following parabolas (and more) are solutions to the problem.
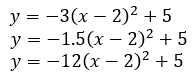
| ||
The y-intercept is the location where a relation crosses the y-axis. Every point on the y-axis has an x-value equal to zero. Putting these ideas together, we can substitute x = 0 into the equation and solve for the y-value. Here is an example.
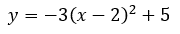
Let x = 0.
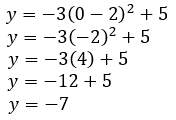
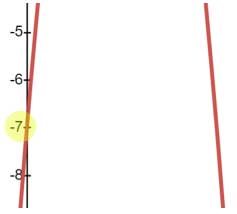
So, the y-intercept for the given parabola is (0,-7). Graphing the parabola, we can see the algebra matches the actual y-intercept. Here is a portion of the graph that shows its y-intercept.
| ||
Here is a parabola in vertex form.
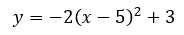
If we were asked to transform this parabola from vertex form to standard form, we would need to follow the order of operations and use a bit of algebra along the way. The order of operations tells us that we must use exponents before we multiply and add. So, we will multiply (x - 5)(x - 5). Here is a multiplication table for that task.
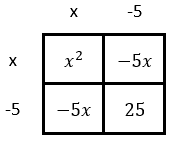
Now we can replace the (x - 5)2 with the four terms from the table.
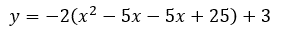
Next, we can add like terms and use the distributive property.
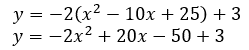
For the last step, we can add like terms.
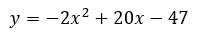
Finally, the parabola is in standard form. Use the link below to try your own problem. | ||
Here is a quizmaster related to the lesson above. | ||
| ||
 esson:
esson:  uiz:
uiz: